Adaptive Unscented Kalman Filter under Minimum Error Entropy with Fiducial Points for Non-Gaussian Systems
Paper and Code
Sep 18, 2023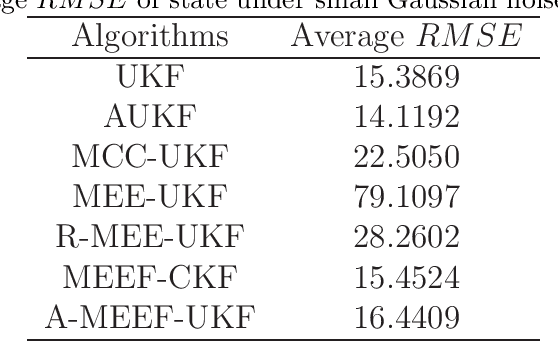
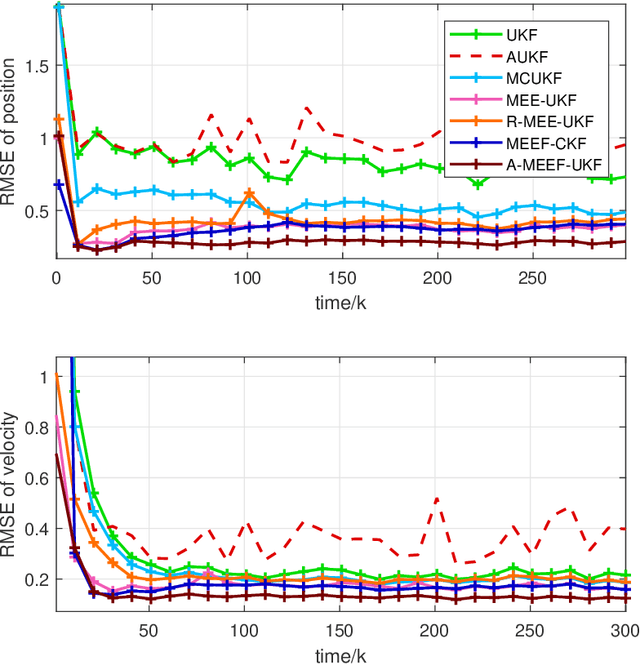
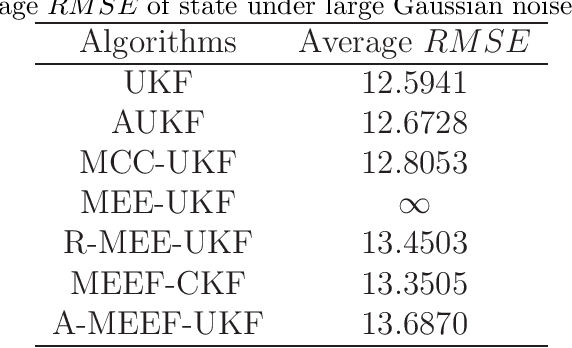
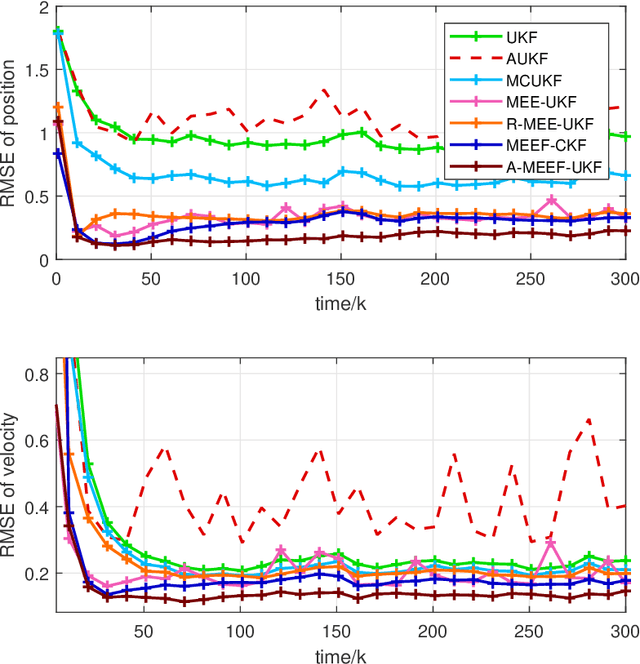
The minimum error entropy (MEE) has been extensively used in unscented Kalman filter (UKF) to handle impulsive noises or abnormal measurement data in non-Gaussian systems. However, the MEE-UKF has poor numerical stability due to the inverse operation of singular matrix. In this paper, a novel UKF based on minimum error entropy with fiducial points (MEEF) is proposed \textcolor{black}{to improve the problem of non-positive definite key matrix. By adding the correntropy to the error entropy, the proposed algorithm further enhances the ability of suppressing impulse noise and outliers. At the same time, considering the uncertainty of noise distribution, the modified Sage-Husa estimator of noise statistics is introduced to adaptively update the noise covariance matrix. In addition, the convergence analysis of the proposed algorithm provides a guidance for the selection of kernel width. The robustness and estimation accuracy of the proposed algorithm are manifested by the state tracking examples under complex non-Gaussian noises.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge