Adaptive Task Allocation for Asynchronous Federated Mobile Edge Learning

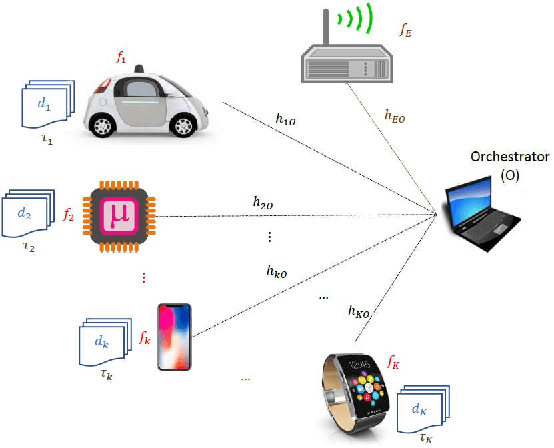
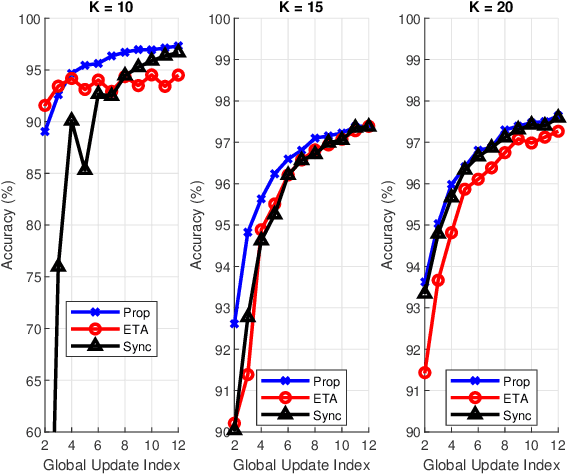
This paper proposes a scheme to efficiently execute distributed learning tasks in an asynchronous manner while minimizing the gradient staleness on wireless edge nodes with heterogeneous computing and communication capacities. The designed approach considered in this paper ensures that all devices work for a certain duration that covers the time for data/model distribution, learning iterations, model collection and global aggregation. The resulting problem is an integer non-convex program with quadratic equality constraints as well as linear equality and inequality constraints. Because the problem is NP-hard, we relax the integer constraints in order to solve it efficiently with available solvers. Analytical bounds are derived using the KKT conditions and Lagrangian analysis in conjunction with the suggest-and-improve approach. Results show that our approach reduces the gradient staleness and can offer better accuracy than the synchronous scheme and the asynchronous scheme with equal task allocation.