Adaptive multi-penalty regularization based on a generalized Lasso path
Paper and Code
Oct 11, 2017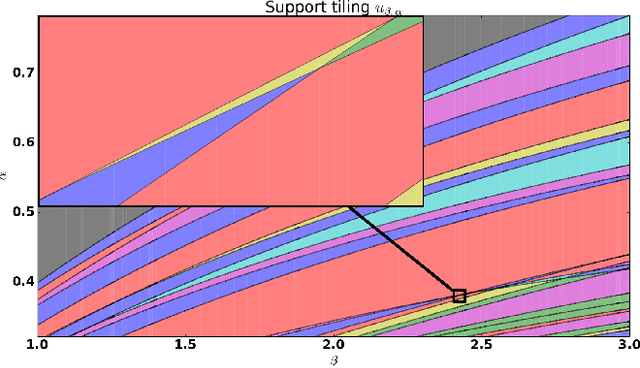
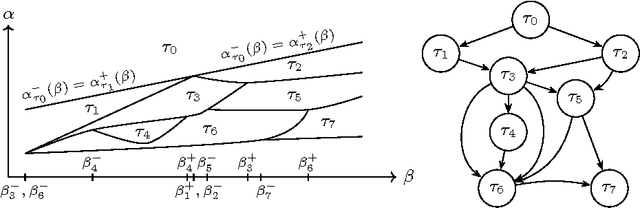
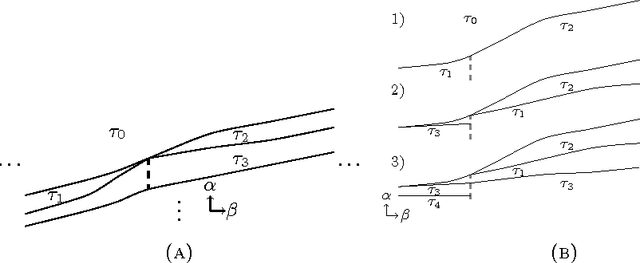
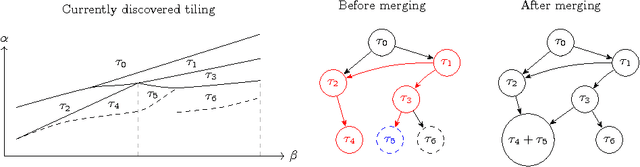
For many algorithms, parameter tuning remains a challenging and critical task, which becomes tedious and infeasible in a multi-parameter setting. Multi-penalty regularization, successfully used for solving undetermined sparse regression of problems of unmixing type where signal and noise are additively mixed, is one of such examples. In this paper, we propose a novel algorithmic framework for an adaptive parameter choice in multi-penalty regularization with a focus on the correct support recovery. Building upon the theory of regularization paths and algorithms for single-penalty functionals, we extend these ideas to a multi-penalty framework by providing an efficient procedure for the construction of regions containing structurally similar solutions, i.e., solutions with the same sparsity and sign pattern, over the whole range of parameters. Combining this with a model selection criterion, we can choose regularization parameters in a data-adaptive manner. Another advantage of our algorithm is that it provides an overview on the solution stability over the whole range of parameters. This can be further exploited to obtain additional insights into the problem of interest. We provide a numerical analysis of our method and compare it to the state-of-the-art single-penalty algorithms for compressed sensing problems in order to demonstrate the robustness and power of the proposed algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge