Adaptive Low-Rank Regularization with Damping Sequences to Restrict Lazy Weights in Deep Networks
Paper and Code
Jun 17, 2021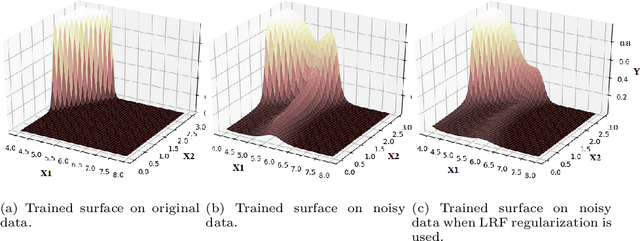
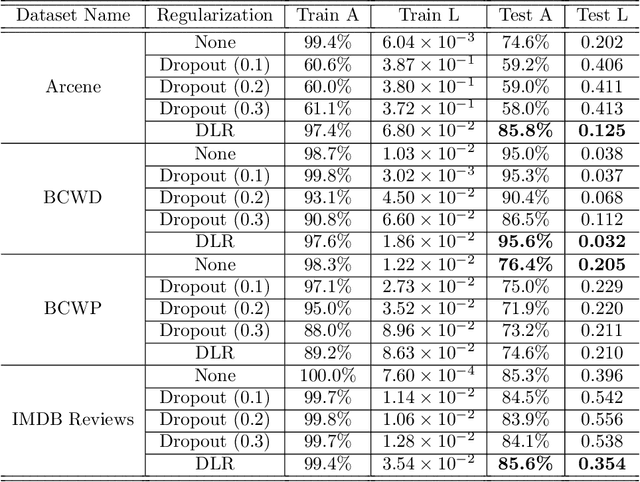
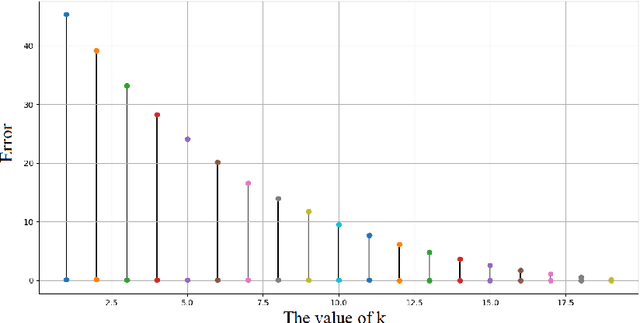
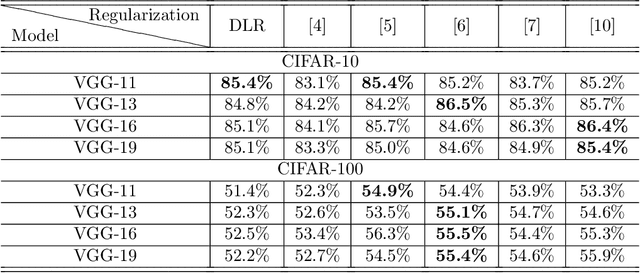
Overfitting is one of the critical problems in deep neural networks. Many regularization schemes try to prevent overfitting blindly. However, they decrease the convergence speed of training algorithms. Adaptive regularization schemes can solve overfitting more intelligently. They usually do not affect the entire network weights. This paper detects a subset of the weighting layers that cause overfitting. The overfitting recognizes by matrix and tensor condition numbers. An adaptive regularization scheme entitled Adaptive Low-Rank (ALR) is proposed that converges a subset of the weighting layers to their Low-Rank Factorization (LRF). It happens by minimizing a new Tikhonov-based loss function. ALR also encourages lazy weights to contribute to the regularization when epochs grow up. It uses a damping sequence to increment layer selection likelihood in the last generations. Thus before falling the training accuracy, ALR reduces the lazy weights and regularizes the network substantially. The experimental results show that ALR regularizes the deep networks well with high training speed and low resource usage.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge