Active Sensing as Bayes-Optimal Sequential Decision Making
Paper and Code
Aug 09, 2014
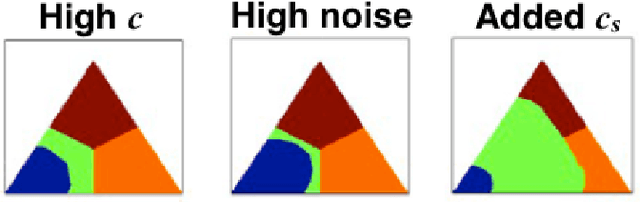
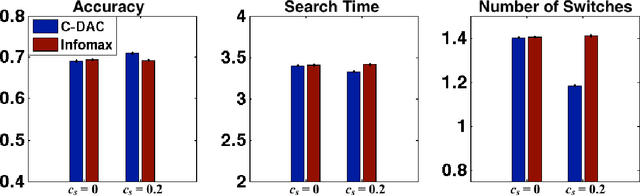
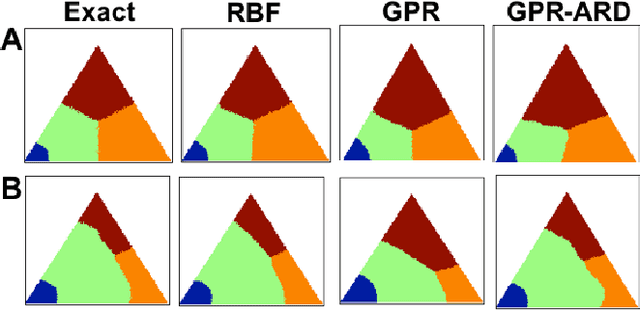
Sensory inference under conditions of uncertainty is a major problem in both machine learning and computational neuroscience. An important but poorly understood aspect of sensory processing is the role of active sensing. Here, we present a Bayes-optimal inference and control framework for active sensing, C-DAC (Context-Dependent Active Controller). Unlike previously proposed algorithms that optimize abstract statistical objectives such as information maximization (Infomax) [Butko & Movellan, 2010] or one-step look-ahead accuracy [Najemnik & Geisler, 2005], our active sensing model directly minimizes a combination of behavioral costs, such as temporal delay, response error, and effort. We simulate these algorithms on a simple visual search task to illustrate scenarios in which context-sensitivity is particularly beneficial and optimization with respect to generic statistical objectives particularly inadequate. Motivated by the geometric properties of the C-DAC policy, we present both parametric and non-parametric approximations, which retain context-sensitivity while significantly reducing computational complexity. These approximations enable us to investigate the more complex problem involving peripheral vision, and we notice that the difference between C-DAC and statistical policies becomes even more evident in this scenario.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge