Achievable Rates for Pattern Recognition
Paper and Code
Sep 08, 2005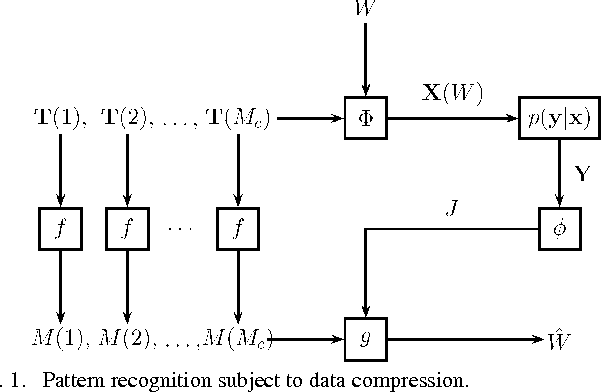
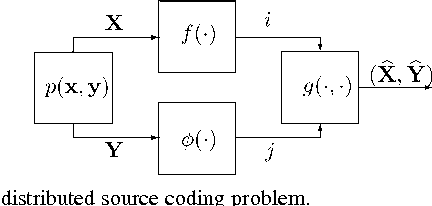
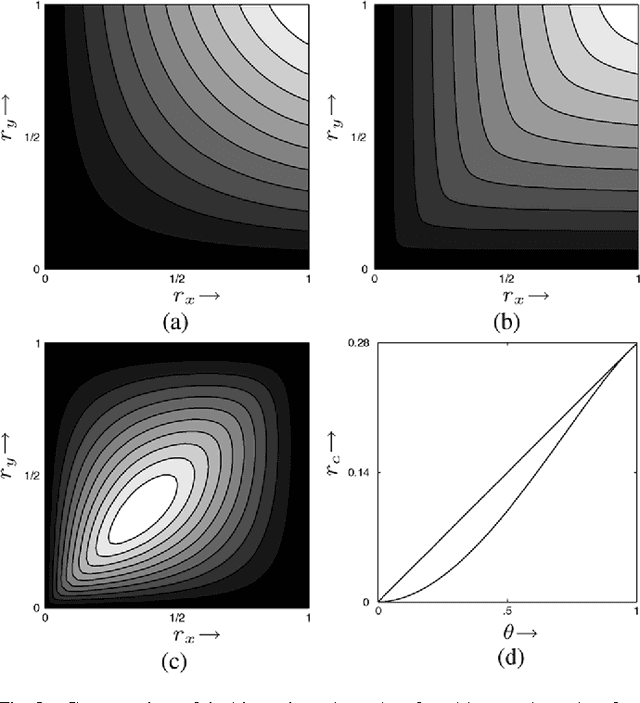
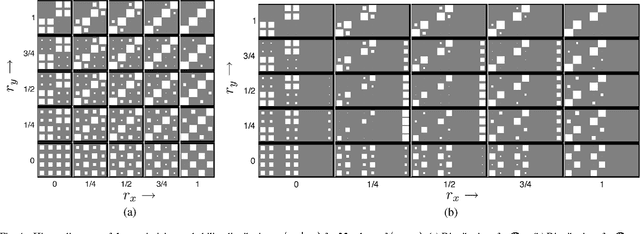
Biological and machine pattern recognition systems face a common challenge: Given sensory data about an unknown object, classify the object by comparing the sensory data with a library of internal representations stored in memory. In many cases of interest, the number of patterns to be discriminated and the richness of the raw data force recognition systems to internally represent memory and sensory information in a compressed format. However, these representations must preserve enough information to accommodate the variability and complexity of the environment, or else recognition will be unreliable. Thus, there is an intrinsic tradeoff between the amount of resources devoted to data representation and the complexity of the environment in which a recognition system may reliably operate. In this paper we describe a general mathematical model for pattern recognition systems subject to resource constraints, and show how the aforementioned resource-complexity tradeoff can be characterized in terms of three rates related to number of bits available for representing memory and sensory data, and the number of patterns populating a given statistical environment. We prove single-letter information theoretic bounds governing the achievable rates, and illustrate the theory by analyzing the elementary cases where the pattern data is either binary or Gaussian.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge