Accelerated Sparse Bayesian Learning via Screening Test and Its Applications
Paper and Code
Jul 08, 2020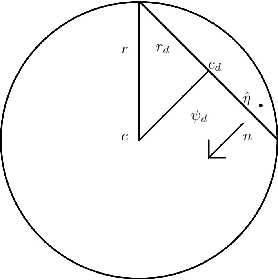
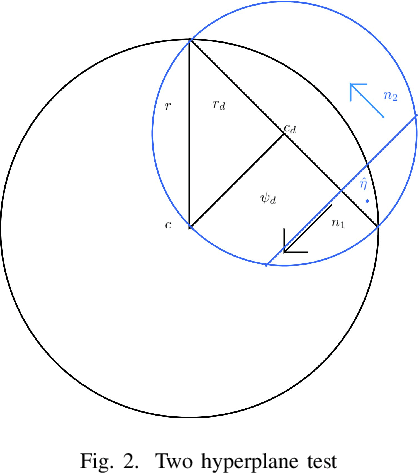
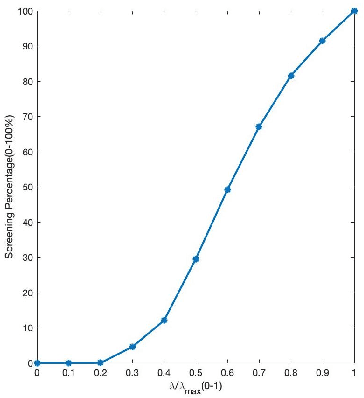
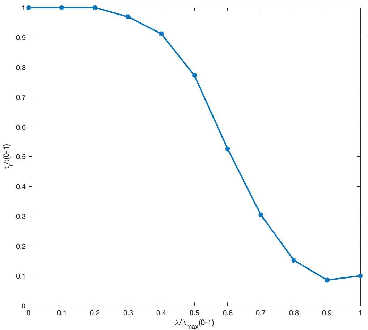
In high-dimensional settings, sparse structures are critical for efficiency in term of memory and computation complexity. For a linear system, to find the sparsest solution provided with an over-complete dictionary of features directly is typically NP-hard, and thus alternative approximate methods should be considered. In this paper, our choice for alternative method is sparse Bayesian learning, which, as empirical Bayesian approaches, uses a parameterized prior to encourage sparsity in solution, rather than the other methods with fixed priors such as LASSO. Screening test, however, aims at quickly identifying a subset of features whose coefficients are guaranteed to be zero in the optimal solution, and then can be safely removed from the complete dictionary to obtain a smaller, more easily solved problem. Next, we solve the smaller problem, after which the solution of the original problem can be recovered by padding the smaller solution with zeros. The performance of the proposed method will be examined on various data sets and applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge