Accelerated Projected Gradient Method for the Optimization of Cell-Free Massive MIMO Downlink
Paper and Code
Jan 12, 2022
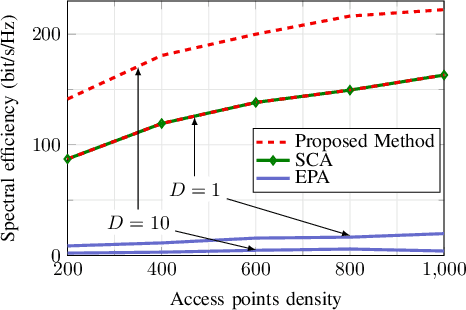

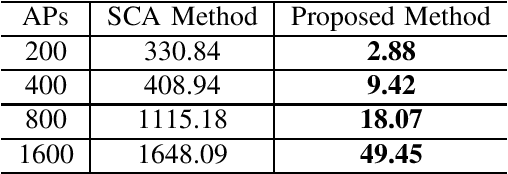
We consider the downlink of a cell-free massive multiple-input multiple-output (MIMO) system where large number of access points (APs) simultaneously serve a group of users. Two fundamental problems are of interest, namely (i) to maximize the total spectral efficiency (SE), and (ii) to maximize the minimum SE of all users. As the considered problems are non-convex, existing solutions rely on successive convex approximation to find a sub-optimal solution. The known methods use off-the-shelf convex solvers, which basically implement an interior-point algorithm, to solve the derived convex problems. The main issue of such methods is that their complexity does not scale favorably with the problem size, limiting previous studies to cell-free massive MIMO of moderate scales. Thus the potential of cell-free massive MIMO has not been fully understood. To address this issue, we propose an accelerated projected gradient method to solve the considered problems. Particularly, the proposed solution is found in closed-form expressions and only requires the first order information of the objective, rather than the Hessian matrix as in known solutions, and thus is much more memory efficient. Numerical results demonstrate that our proposed solution achieves far less run-time, compared to other second-order methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge