Absolute Shapley Value
Paper and Code
Mar 23, 2020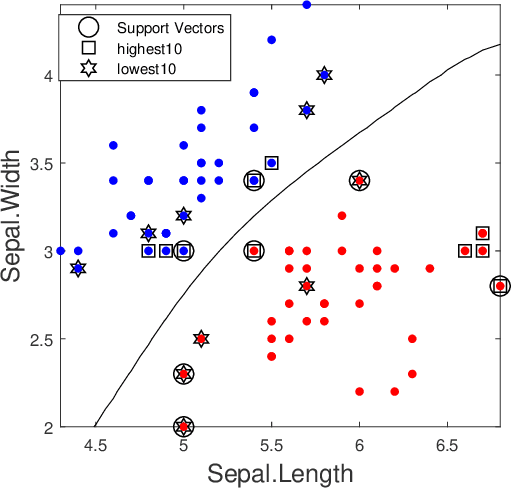
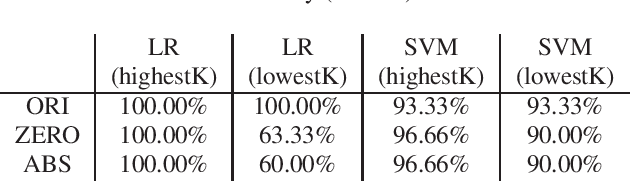
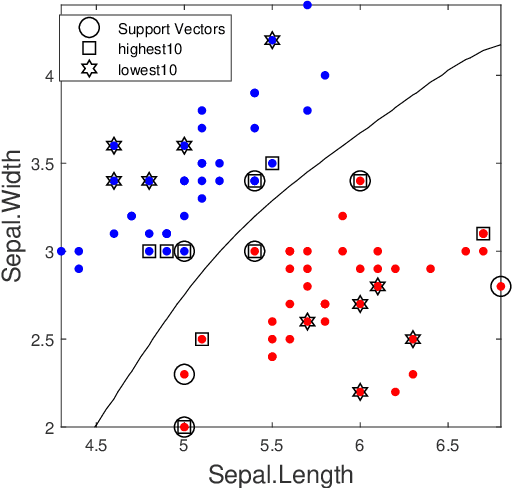

Shapley value is a concept in cooperative game theory for measuring the contribution of each participant, which was named in honor of Lloyd Shapley. Shapley value has been recently applied in data marketplaces for compensation allocation based on their contribution to the models. Shapley value is the only value division scheme used for compensation allocation that meets three desirable criteria: group rationality, fairness, and additivity. In cooperative game theory, the marginal contribution of each contributor to each coalition is a nonnegative value. However, in machine learning model training, the marginal contribution of each contributor (data tuple) to each coalition (a set of data tuples) can be a negative value, i.e., the accuracy of the model trained by a dataset with an additional data tuple can be lower than the accuracy of the model trained by the dataset only. In this paper, we investigate the problem of how to handle the negative marginal contribution when computing Shapley value. We explore three philosophies: 1) taking the original value (Original Shapley Value); 2) taking the larger of the original value and zero (Zero Shapley Value); and 3) taking the absolute value of the original value (Absolute Shapley Value). Experiments on Iris dataset demonstrate that the definition of Absolute Shapley Value significantly outperforms the other two definitions in terms of evaluating data importance (the contribution of each data tuple to the trained model).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge