A U-statistic Approach to Hypothesis Testing for Structure Discovery in Undirected Graphical Models
Paper and Code
Apr 06, 2016
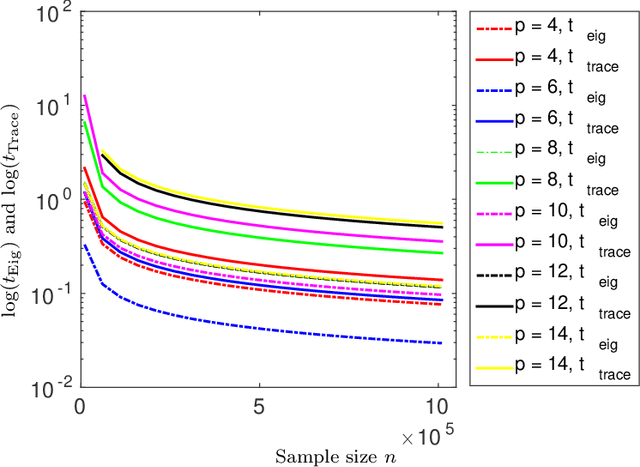
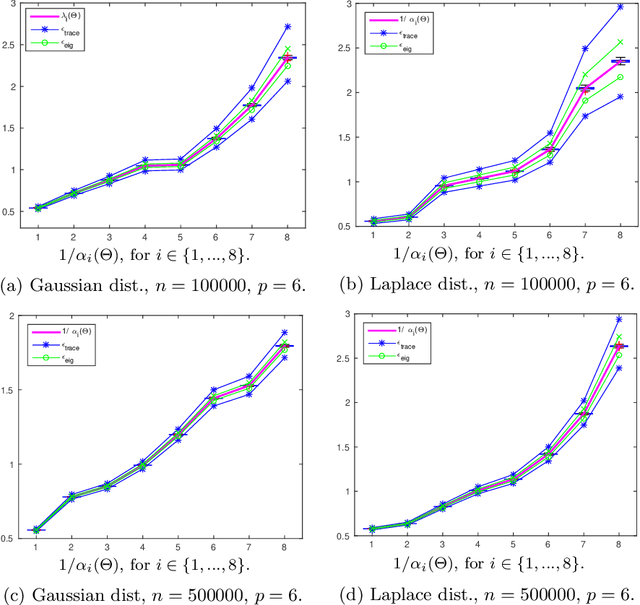
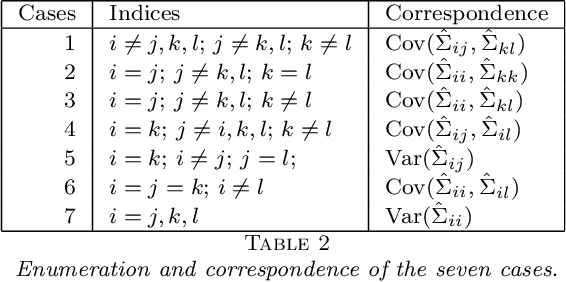
Structure discovery in graphical models is the determination of the topology of a graph that encodes conditional independence properties of the joint distribution of all variables in the model. For some class of probability distributions, an edge between two variables is present if and only if the corresponding entry in the precision matrix is non-zero. For a finite sample estimate of the precision matrix, entries close to zero may be due to low sample effects, or due to an actual association between variables; these two cases are not readily distinguishable. %Fisher provided a hypothesis test based on a parametric approximation to the distribution of an entry in the precision matrix of a Gaussian distribution, but this may not provide valid upper bounds on $p$-values for non-Gaussian distributions. Many related works on this topic consider potentially restrictive distributional or sparsity assumptions that may not apply to a data sample of interest, and direct estimation of the uncertainty of an estimate of the precision matrix for general distributions remains challenging. Consequently, we make use of results for $U$-statistics and apply them to the covariance matrix. By probabilistically bounding the distortion of the covariance matrix, we can apply Weyl's theorem to bound the distortion of the precision matrix, yielding a conservative, but sound test threshold for a much wider class of distributions than considered in previous works. The resulting test enables one to answer with statistical significance whether an edge is present in the graph, and convergence results are known for a wide range of distributions. The computational complexities is linear in the sample size enabling the application of the test to large data samples for which computation time becomes a limiting factor. We experimentally validate the correctness and scalability of the test on multivariate distributions for which the distributional assumptions of competing tests result in underestimates of the false positive ratio. By contrast, the proposed test remains sound, promising to be a useful tool for hypothesis testing for diverse real-world problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge