A Two Parameters Equation for Word Rank-Frequency Relation

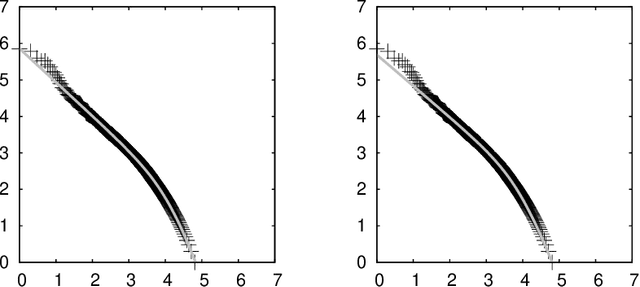
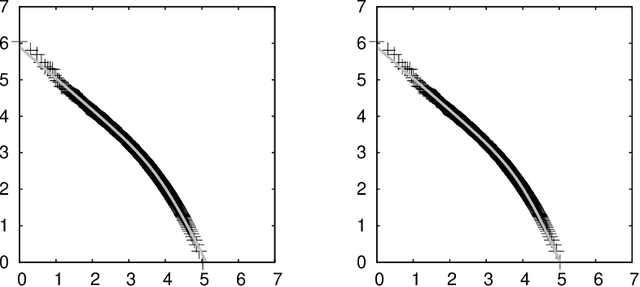
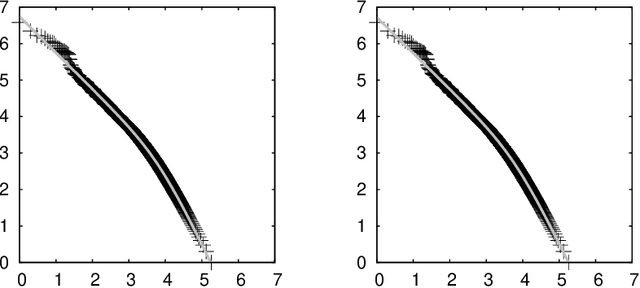
Let $f (\cdot)$ be the absolute frequency of words and $r$ be the rank of words in decreasing order of frequency, then the following function can fit the rank-frequency relation \[ f (r;s,t) = \left(\frac{r_{\tt max}}{r}\right)^{1-s} \left(\frac{r_{\tt max}+t \cdot r_{\tt exp}}{r+t \cdot r_{\tt exp}}\right)^{1+(1+t)s} \] where $r_{\tt max}$ and $r_{\tt exp}$ are the maximum and the expectation of the rank, respectively; $s>0$ and $t>0$ are parameters estimated from data. On well-behaved data, there should be $s<1$ and $s \cdot t < 1$.