A two-dimensional decomposition approach for matrix completion through gossip
Paper and Code
Jan 11, 2018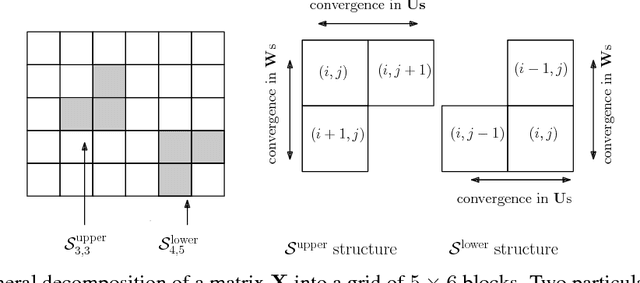


Factoring a matrix into two low rank matrices is at the heart of many problems. The problem of matrix completion especially uses it to decompose a sparse matrix into two non sparse, low rank matrices which can then be used to predict unknown entries of the original matrix. We present a scalable and decentralized approach in which instead of learning two factors for the original input matrix, we decompose the original matrix into a grid blocks, each of whose factors can be individually learned just by communicating (gossiping) with neighboring blocks. This eliminates any need for a central server. We show that our algorithm performs well on both synthetic and real datasets.
* Appeared in the Emergent Communication Workshop at NIPS 2017
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge