A Tractable Algorithm For Finite-Horizon Continuous Reinforcement Learning
Paper and Code
Jun 26, 2019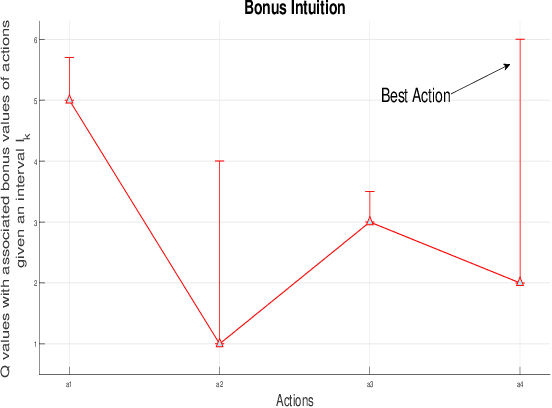
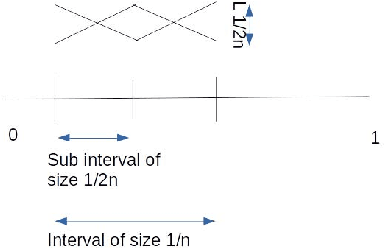


We consider the finite horizon continuous reinforcement learning problem. Our contribution is three-fold. First,we give a tractable algorithm based on optimistic value iteration for the problem. Next,we give a lower bound on regret of order $\Omega(T^{2/3})$ for any algorithm discretizes the state space, improving the previous regret bound of $\Omega(T^{1/2})$ of Ortner and Ryabko \cite{contrl} for the same problem. Next,under the assumption that the rewards and transitions are H\"{o}lder Continuous we show that the upper bound on the discretization error is $const.Ln^{-\alpha}T$. Finally,we give some simple experiments to validate our propositions.
* InProceedings of International Conference on Intelligent Autonomous
System, ICOIAS 2019
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge