A Time-Series Scale Mixture Model of EEG with a Hidden Markov Structure for Epileptic Seizure Detection
Paper and Code
Nov 12, 2021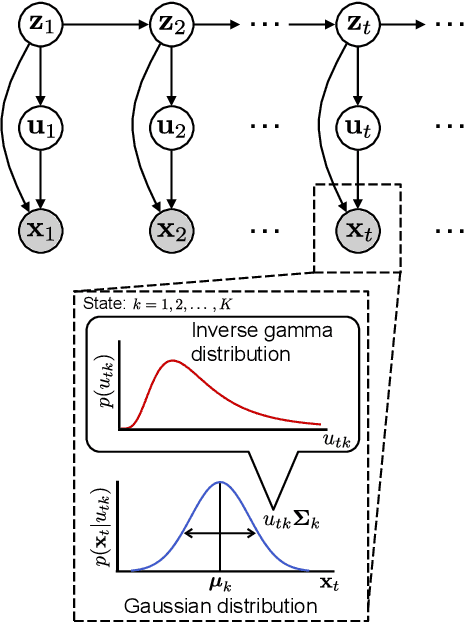
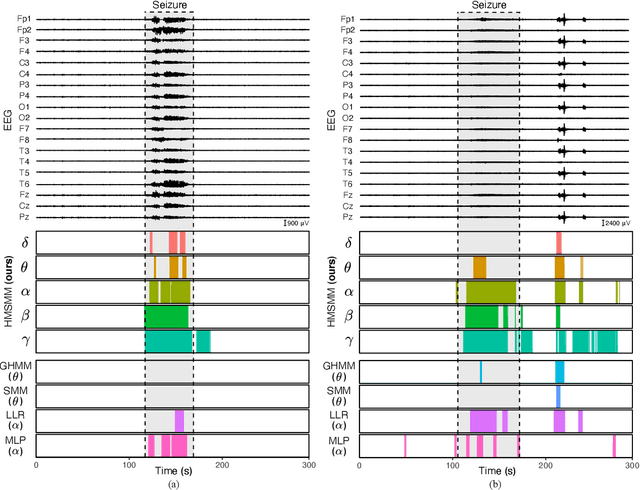
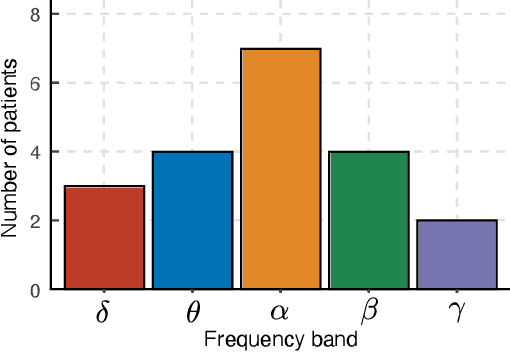
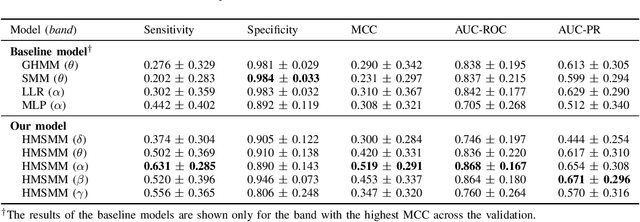
In this paper, we propose a time-series stochastic model based on a scale mixture distribution with Markov transitions to detect epileptic seizures in electroencephalography (EEG). In the proposed model, an EEG signal at each time point is assumed to be a random variable following a Gaussian distribution. The covariance matrix of the Gaussian distribution is weighted with a latent scale parameter, which is also a random variable, resulting in the stochastic fluctuations of covariances. By introducing a latent state variable with a Markov chain in the background of this stochastic relationship, time-series changes in the distribution of latent scale parameters can be represented according to the state of epileptic seizures. In an experiment, we evaluated the performance of the proposed model for seizure detection using EEGs with multiple frequency bands decomposed from a clinical dataset. The results demonstrated that the proposed model can detect seizures with high sensitivity and outperformed several baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge