A time series distance measure for efficient clustering of input output signals by their underlying dynamics
Paper and Code
Mar 06, 2017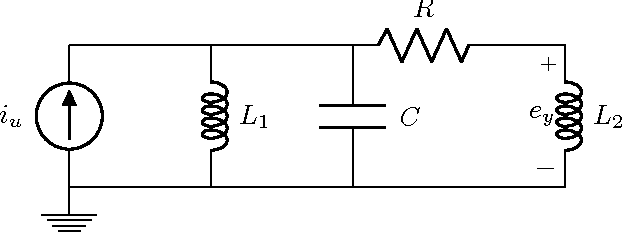
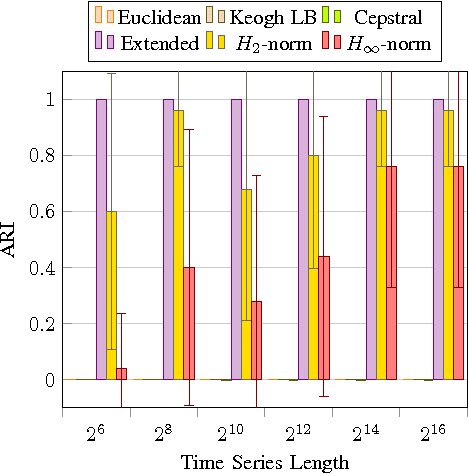
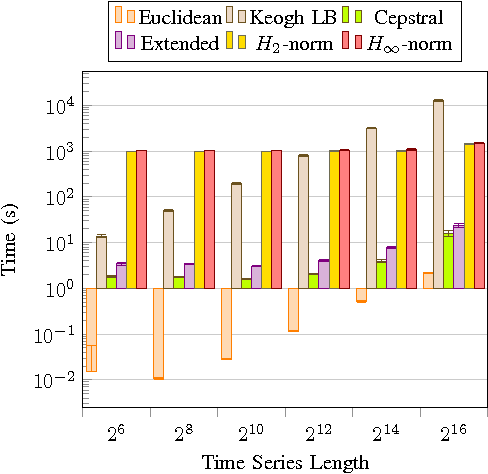
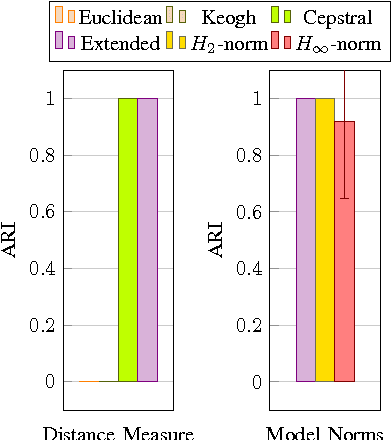
Starting from a dataset with input/output time series generated by multiple deterministic linear dynamical systems, this paper tackles the problem of automatically clustering these time series. We propose an extension to the so-called Martin cepstral distance, that allows to efficiently cluster these time series, and apply it to simulated electrical circuits data. Traditionally, two ways of handling the problem are used. The first class of methods employs a distance measure on time series (e.g. Euclidean, Dynamic Time Warping) and a clustering technique (e.g. k-means, k-medoids, hierarchical clustering) to find natural groups in the dataset. It is, however, often not clear whether these distance measures effectively take into account the specific temporal correlations in these time series. The second class of methods uses the input/output data to identify a dynamic system using an identification scheme, and then applies a model norm-based distance (e.g. H2, H-infinity) to find out which systems are similar. This, however, can be very time consuming for large amounts of long time series data. We show that the new distance measure presented in this paper performs as good as when every input/output pair is modelled explicitly, but remains computationally much less complex. The complexity of calculating this distance between two time series of length N is O(N logN).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge