A Temporal-Difference Approach to Policy Gradient Estimation
Paper and Code
Feb 04, 2022
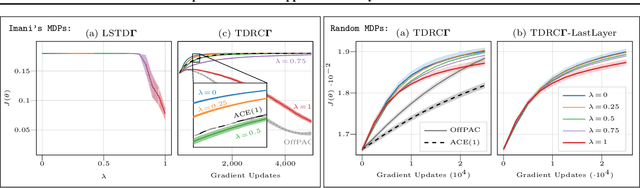
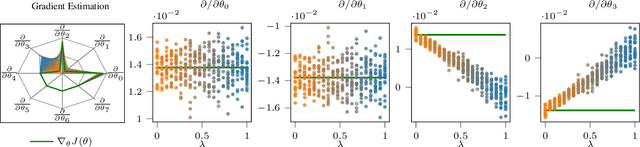
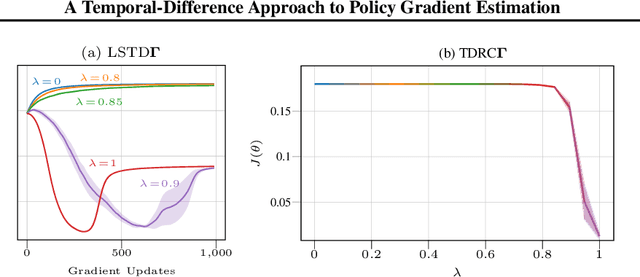
The policy gradient theorem (Sutton et al., 2000) prescribes the usage of a cumulative discounted state distribution under the target policy to approximate the gradient. Most algorithms based on this theorem, in practice, break this assumption, introducing a distribution shift that can cause the convergence to poor solutions. In this paper, we propose a new approach of reconstructing the policy gradient from the start state without requiring a particular sampling strategy. The policy gradient calculation in this form can be simplified in terms of a gradient critic, which can be recursively estimated due to a new Bellman equation of gradients. By using temporal-difference updates of the gradient critic from an off-policy data stream, we develop the first estimator that sidesteps the distribution shift issue in a model-free way. We prove that, under certain realizability conditions, our estimator is unbiased regardless of the sampling strategy. We empirically show that our technique achieves a superior bias-variance trade-off and performance in presence of off-policy samples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge