A Step Towards Uncovering The Structure of Multistable Neural Networks

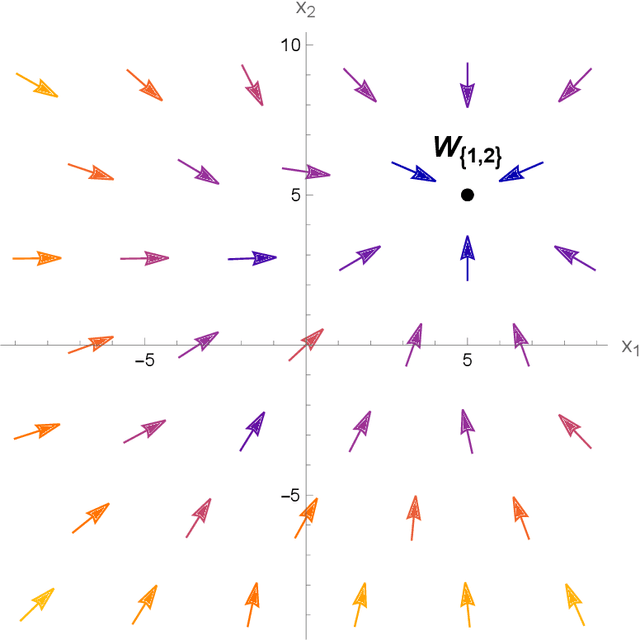
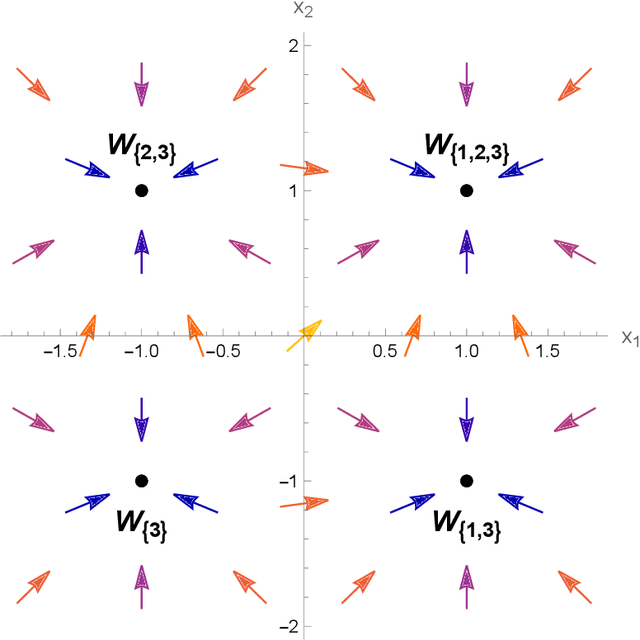
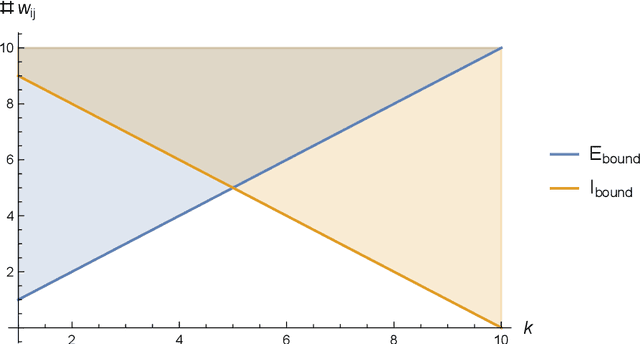
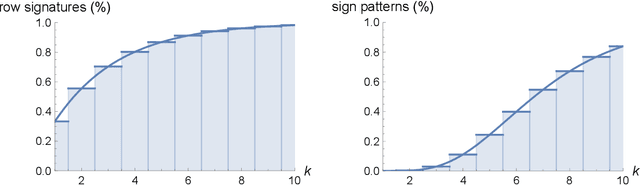
We study the structure of multistable recurrent neural networks. The activation function is simplified by a nonsmooth Heaviside step function. This nonlinearity partitions the phase space into regions with different, yet linear dynamics. We derive how multistability is encoded within the network architecture. Stable states are identified by their semipositivity constraints on the synaptic weight matrix. The restrictions can be separated by their effects on the signs or the strengths of the connections. Exact results on network topology, sign stability, weight matrix factorization, pattern completion and pattern coupling are derived and proven. These may lay the foundation of more complex recurrent neural networks and neurocomputing.