A Single-Timescale Analysis For Stochastic Approximation With Multiple Coupled Sequences
Paper and Code
Jun 21, 2022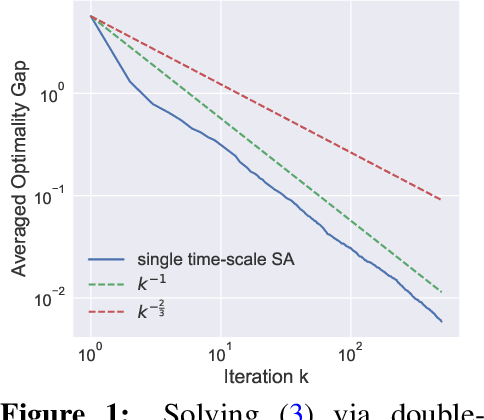

Stochastic approximation (SA) with multiple coupled sequences has found broad applications in machine learning such as bilevel learning and reinforcement learning (RL). In this paper, we study the finite-time convergence of nonlinear SA with multiple coupled sequences. Different from existing multi-timescale analysis, we seek for scenarios where a fine-grained analysis can provide the tight performance guarantee for multi-sequence single-timescale SA (STSA). At the heart of our analysis is the smoothness property of the fixed points in multi-sequence SA that holds in many applications. When all sequences have strongly monotone increments, we establish the iteration complexity of $\mathcal{O}(\epsilon^{-1})$ to achieve $\epsilon$-accuracy, which improves the existing $\mathcal{O}(\epsilon^{-1.5})$ complexity for two coupled sequences. When all but the main sequence have strongly monotone increments, we establish the iteration complexity of $\mathcal{O}(\epsilon^{-2})$. The merit of our results lies in that applying them to stochastic bilevel and compositional optimization problems, as well as RL problems leads to either relaxed assumptions or improvements over their existing performance guarantees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge