A Simple Sparse Matrix Vector Multiplication Approach to Padded Convolution
Paper and Code
Nov 29, 2024
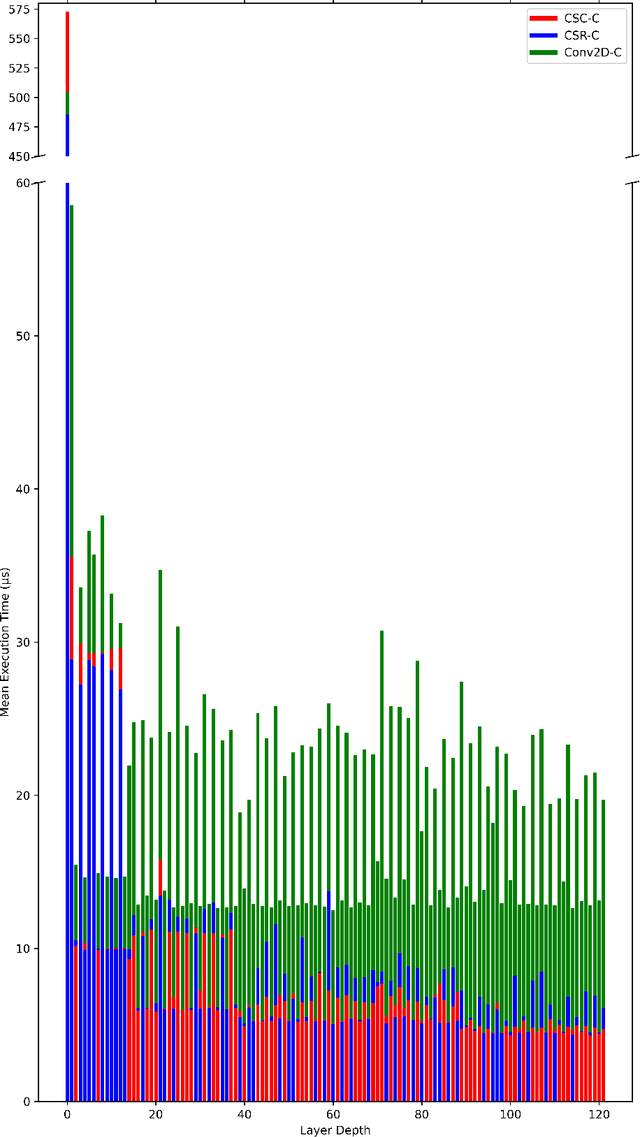


We introduce an algorithm for efficiently representing convolution with zero-padding and stride as a sparse transformation matrix, applied to a vectorized input through sparse matrix-vector multiplication (SpMV). We provide a theoretical contribution with an explicit expression for the number of non-zero multiplications in convolutions with stride and padding, offering insight into the potential for leveraging sparsity in convolution operations. A proof-of-concept implementation is presented in Python, demonstrating the performance of our method on both CPU and GPU architectures. This work contributes to the broader exploration of sparse matrix techniques in convolutional algorithms, with a particular focus on leveraging matrix multiplications for parallelization. Our findings lay the groundwork for future advancements in exploiting sparsity to improve the efficiency of convolution operations in fields such as machine learning and signal processing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge