A Robust Scientific Machine Learning for Optimization: A Novel Robustness Theorem
Paper and Code
Sep 13, 2022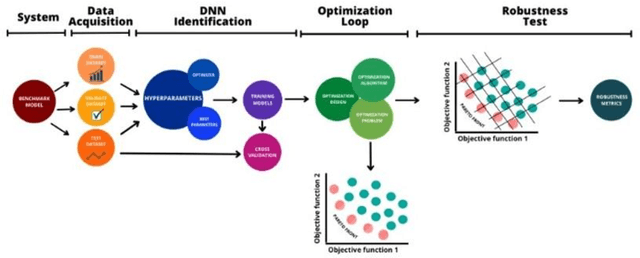

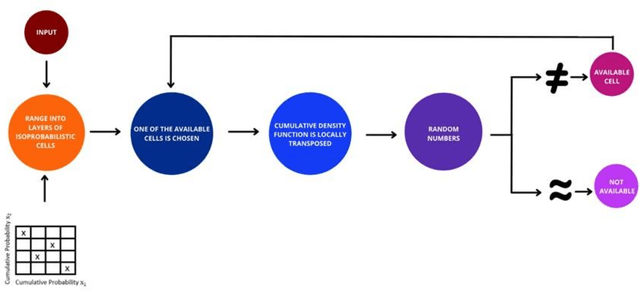
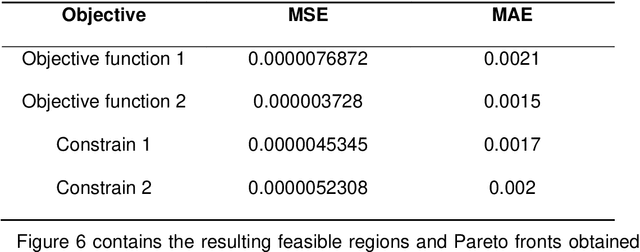
Scientific machine learning (SciML) is a field of increasing interest in several different application fields. In an optimization context, SciML-based tools have enabled the development of more efficient optimization methods. However, implementing SciML tools for optimization must be rigorously evaluated and performed with caution. This work proposes the deductions of a robustness test that guarantees the robustness of multiobjective SciML-based optimization by showing that its results respect the universal approximator theorem. The test is applied in the framework of a novel methodology which is evaluated in a series of benchmarks illustrating its consistency. Moreover, the proposed methodology results are compared with feasible regions of rigorous optimization, which requires a significantly higher computational effort. Hence, this work provides a robustness test for guaranteed robustness in applying SciML tools in multiobjective optimization with lower computational effort than the existent alternative.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge