A Review and Evaluation of Elastic Distance Functions for Time Series Clustering
Paper and Code
May 30, 2022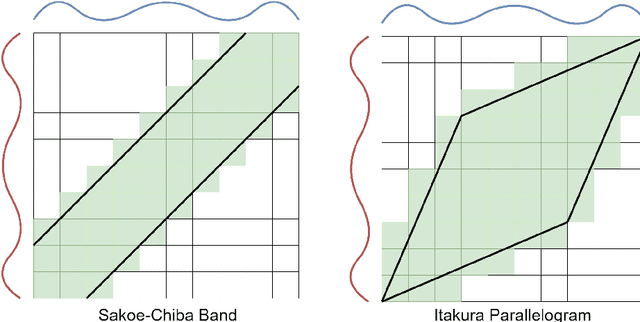
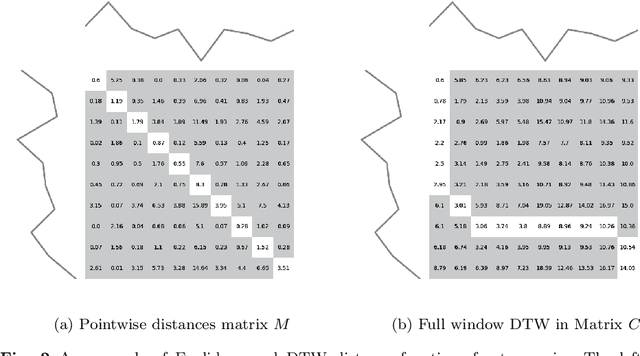
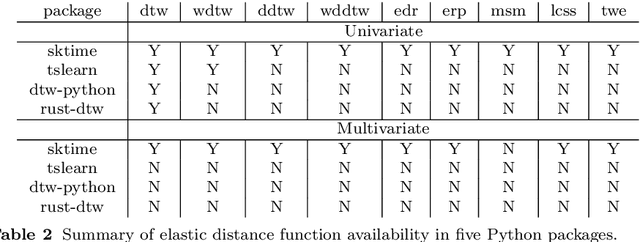
Time series clustering is the act of grouping time series data without recourse to a label. Algorithms that cluster time series can be classified into two groups: those that employ a time series specific distance measure; and those that derive features from time series. Both approaches usually rely on traditional clustering algorithms such as $k$-means. Our focus is on distance based time series that employ elastic distance measures, i.e. distances that perform some kind of realignment whilst measuring distance. We describe nine commonly used elastic distance measures and compare their performance with k-means and k-medoids clustering. Our findings are surprising. The most popular technique, dynamic time warping (DTW), performs worse than Euclidean distance with k-means, and even when tuned, is no better. Using k-medoids rather than k-means improved the clusterings for all nine distance measures. DTW is not significantly better than Euclidean distance with k-medoids. Generally, distance measures that employ editing in conjunction with warping perform better, and one distance measure, the move-split-merge (MSM) method, is the best performing measure of this study. We also compare to clustering with DTW using barycentre averaging (DBA). We find that DBA does improve DTW k-means, but that the standard DBA is still worse than using MSM. Our conclusion is to recommend MSM with k-medoids as the benchmark algorithm for clustering time series with elastic distance measures. We provide implementations, results and guidance on reproducing results on the associated GitHub repository.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge