A Reinforcement Learning Approach to the Orienteering Problem with Time Windows

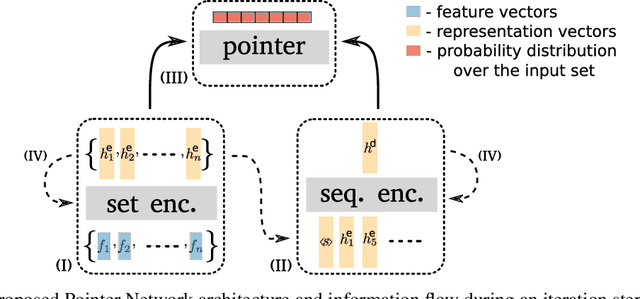
The Orienteering Problem with Time Windows (OPTW) is a combinatorial optimization problem where the goal is to maximize the total scores collected from visited locations, under some time constraints. Several heuristics have been proposed for the OPTW, yet in comparison with machine learning models, a heuristic typically has a smaller potential for generalization and personalization. The application of neural network models to combinatorial optimization has recently shown promising results in similar problems like the Travelling Salesman Problem. A neural network allows learning solutions using reinforcement learning or in a supervised way, depending on the available data. After learning, it can potentially generalize and be quickly fine-tuned to further improve performance and personalization. This is advantageous since, for real word applications, a solution's quality, personalization and execution times are all important factors to be taken into account. Here we explore the use of Pointer Network models trained with reinforcement learning for solving the OPTW problem. Among its various applications, the OPTW can be used to model the Tourist Trip Design Problem (TTDP). We train the Pointer Network with the TTDP problem in mind, by sampling variables that can change across tourists for a particular instance-region: starting position, starting time, time available and the scores of each point of interest. After a model-region is trained it can infer a solution for a particular tourist using beam search. We evaluate our approach on several existing benchmark OPTW instances. We show that it is able to generalize across different generated tourists for each region and that it generally outperforms the most commonly used heuristic while computing the solution in realistic times.