A preliminary analysis on metaheuristics methods applied to the Haplotype Inference Problem
Paper and Code
Aug 03, 2007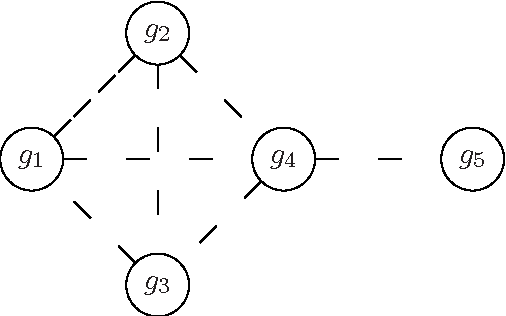
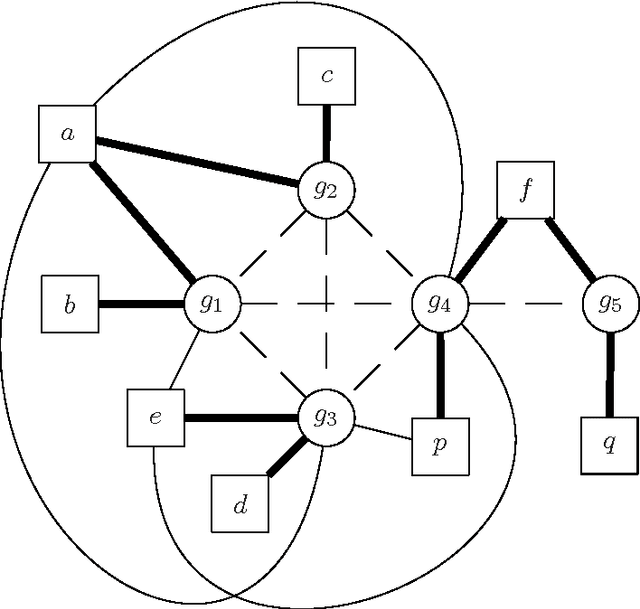
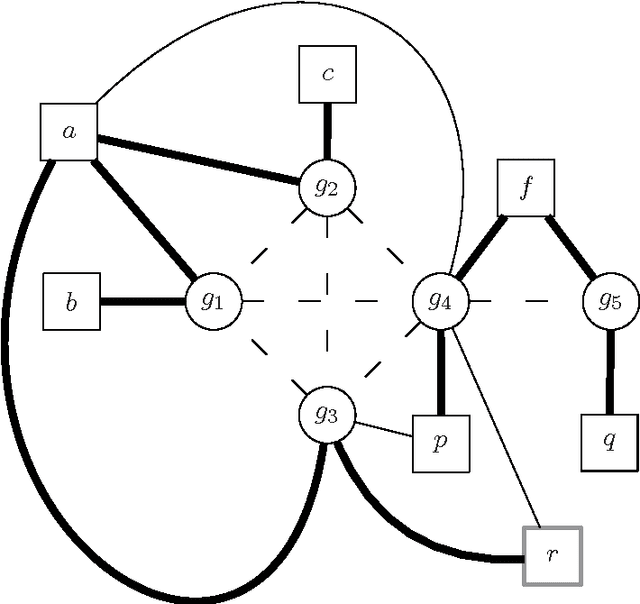
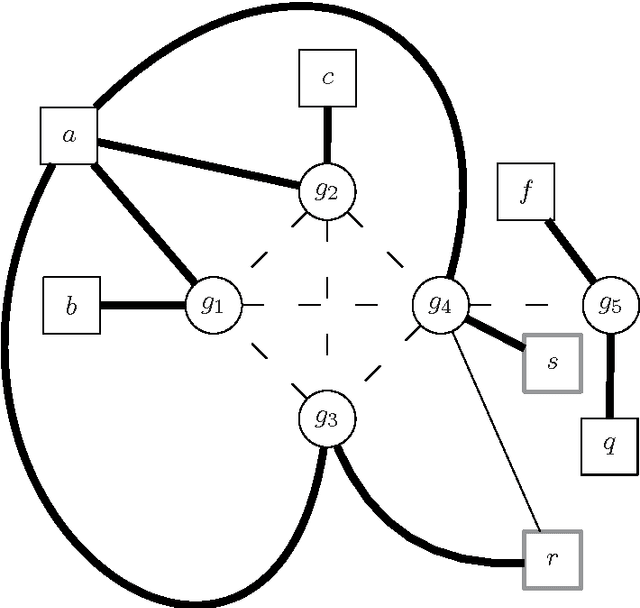
Haplotype Inference is a challenging problem in bioinformatics that consists in inferring the basic genetic constitution of diploid organisms on the basis of their genotype. This information allows researchers to perform association studies for the genetic variants involved in diseases and the individual responses to therapeutic agents. A notable approach to the problem is to encode it as a combinatorial problem (under certain hypotheses, such as the pure parsimony criterion) and to solve it using off-the-shelf combinatorial optimization techniques. The main methods applied to Haplotype Inference are either simple greedy heuristic or exact methods (Integer Linear Programming, Semidefinite Programming, SAT encoding) that, at present, are adequate only for moderate size instances. We believe that metaheuristic and hybrid approaches could provide a better scalability. Moreover, metaheuristics can be very easily combined with problem specific heuristics and they can also be integrated with tree-based search techniques, thus providing a promising framework for hybrid systems in which a good trade-off between effectiveness and efficiency can be reached. In this paper we illustrate a feasibility study of the approach and discuss some relevant design issues, such as modeling and design of approximate solvers that combine constructive heuristics, local search-based improvement strategies and learning mechanisms. Besides the relevance of the Haplotype Inference problem itself, this preliminary analysis is also an interesting case study because the formulation of the problem poses some challenges in modeling and hybrid metaheuristic solver design that can be generalized to other problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge