A Pre-processing Method for Fairness in Ranking
Paper and Code
Oct 29, 2021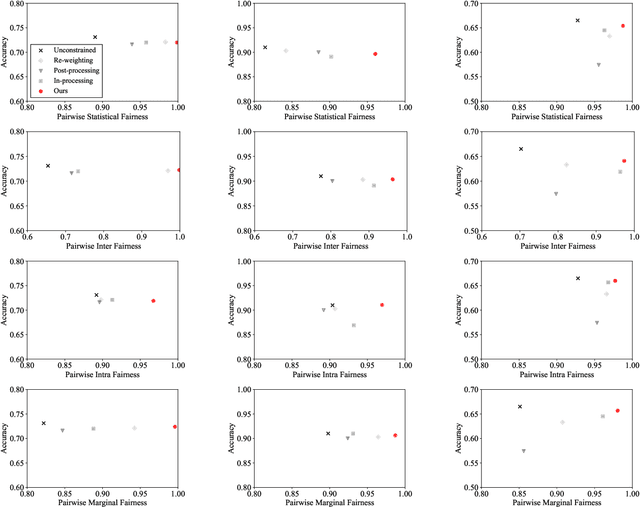
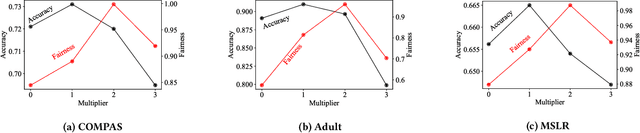
Fair ranking problems arise in many decision-making processes that often necessitate a trade-off between accuracy and fairness. Many existing studies have proposed correction methods such as adding fairness constraints to a ranking model's loss. However, the challenge of correcting the data bias for fair ranking remains, and the trade-off of the ranking models leaves room for improvement. In this paper, we propose a fair ranking framework that evaluates the order of training data in a pairwise manner as well as various fairness measurements in ranking. This study is the first proposal of a pre-processing method that solves fair ranking problems using the pairwise ordering method with our best knowledge. The fair pairwise ordering method is prominent in training the fair ranking models because it ensures that the resulting ranking likely becomes parity across groups. As far as the fairness measurements in ranking are represented as a linear constraint of the ranking models, we proved that the minimization of loss function subject to the constraints is reduced to the closed solution of the minimization problem augmented by weights to training data. This closed solution inspires us to present a practical and stable algorithm that iterates the optimization of weights and model parameters. The empirical results over real-world datasets demonstrated that our method outperforms the existing methods in the trade-off between accuracy and fairness over real-world datasets and various fairness measurements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge