A Panel Quantile Approach to Attrition Bias in Big Data: Evidence from a Randomized Experiment
Paper and Code
Aug 09, 2018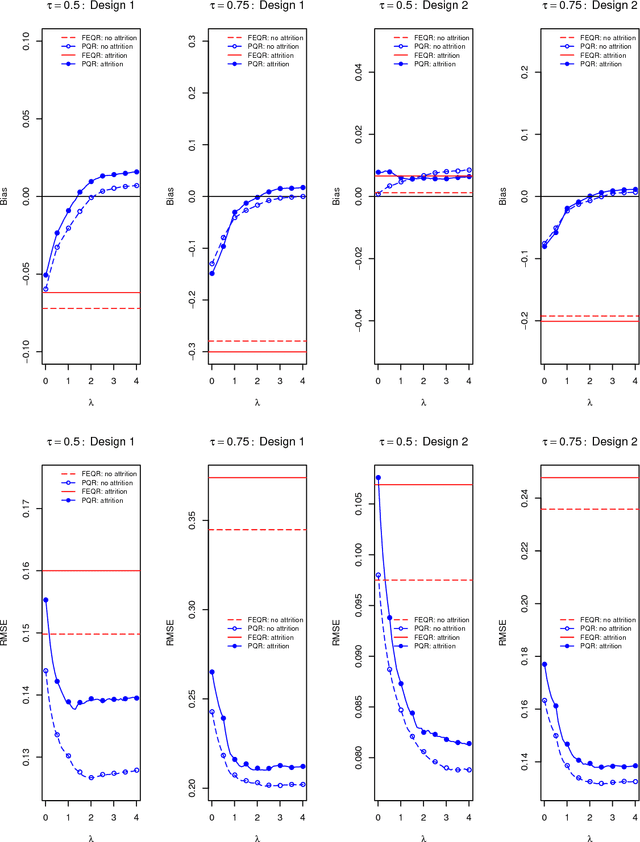
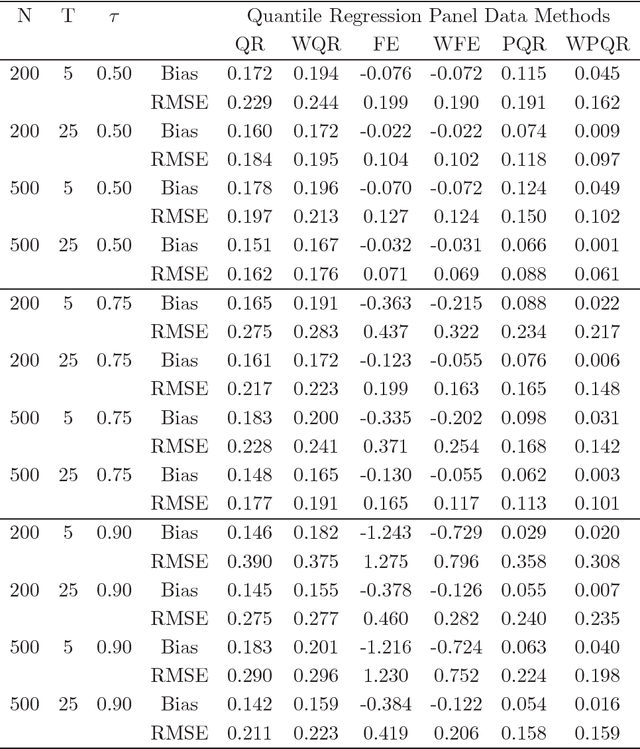
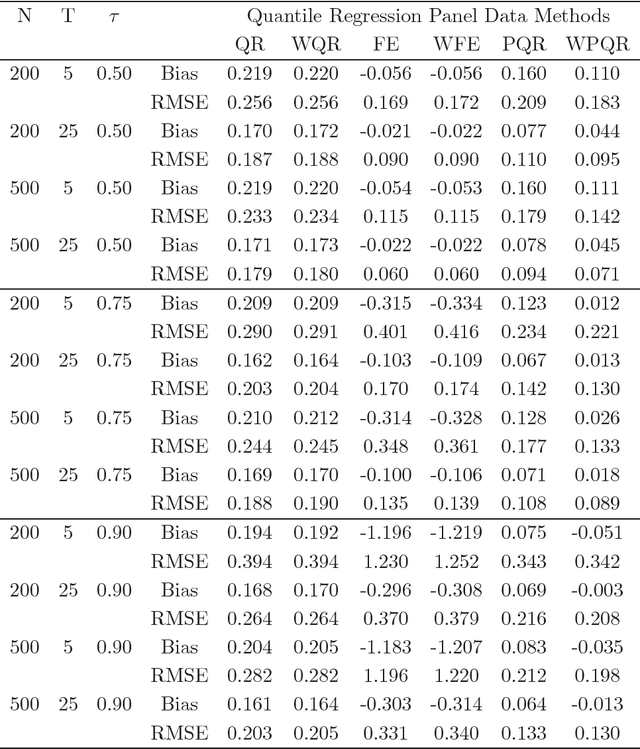
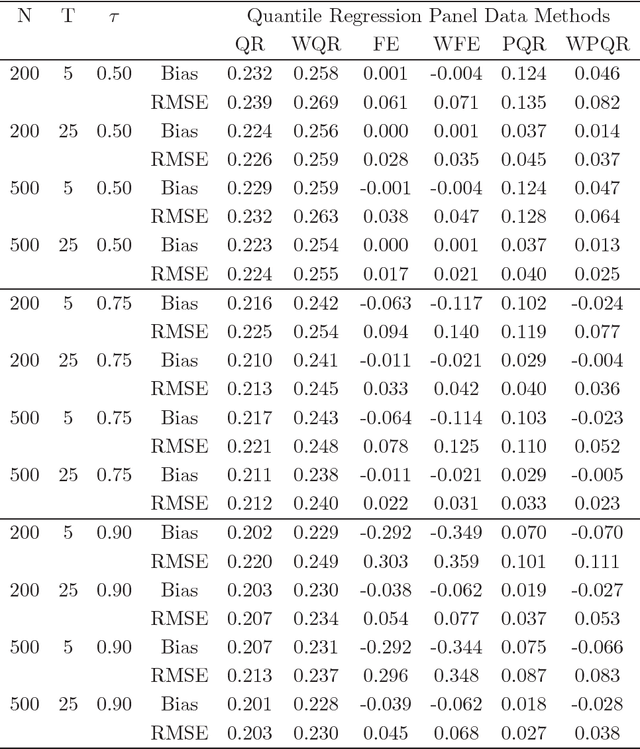
This paper introduces a quantile regression estimator for panel data models with individual heterogeneity and attrition. The method is motivated by the fact that attrition bias is often encountered in Big Data applications. For example, many users sign-up for the latest program but few remain active users several months later, making the evaluation of such interventions inherently very challenging. Building on earlier work by Hausman and Wise (1979), we provide a simple identification strategy that leads to a two-step estimation procedure. In the first step, the coefficients of interest in the selection equation are consistently estimated using parametric or nonparametric methods. In the second step, standard panel quantile methods are employed on a subset of weighted observations. The estimator is computationally easy to implement in Big Data applications with a large number of subjects. We investigate the conditions under which the parameter estimator is asymptotically Gaussian and we carry out a series of Monte Carlo simulations to investigate the finite sample properties of the estimator. Lastly, using a simulation exercise, we apply the method to the evaluation of a recent Time-of-Day electricity pricing experiment inspired by the work of Aigner and Hausman (1980).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge