A Numerical Framework for Efficient Motion Estimation on Evolving Sphere-Like Surfaces based on Brightness and Mass Conservation Laws

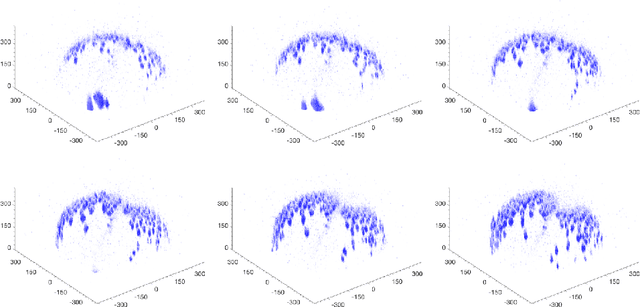
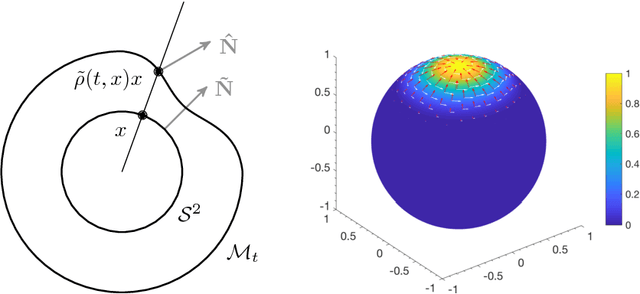
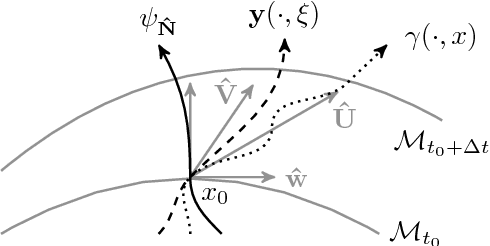
In this work we consider brightness and mass conservation laws for motion estimation on evolving Riemannian 2-manifolds that allow for a radial parametrisation from the 2-sphere. While conservation of brightness constitutes the foundation for optical flow methods and has been generalised to said scenario, we formulate in this article the principle of mass conservation for time-varying surfaces which are embedded in Euclidean 3-space and derive a generalised continuity equation. The main motivation for this work is efficient cell motion estimation in time-lapse (4D) volumetric fluorescence microscopy images of a living zebrafish embryo. Increasing spatial and temporal resolution of modern microscopes require efficient analysis of such data. With this application in mind we address this need and follow an emerging paradigm in this field: dimensional reduction. In light of the ill-posedness of considered conservation laws we employ Tikhonov regularisation and propose the use of spatially varying regularisation functionals that recover motion only in regions with cells. For the efficient numerical solution we devise a Galerkin method based on compactly supported (tangent) vectorial basis functions. Furthermore, for the fast and accurate estimation of the evolving sphere-like surface from scattered data we utilise surface interpolation with spatio-temporal regularisation. We present numerical results based on aforementioned zebrafish microscopy data featuring fluorescently labelled cells.