A Novel Stochastic Stratified Average Gradient Method: Convergence Rate and Its Complexity
Paper and Code
Dec 03, 2017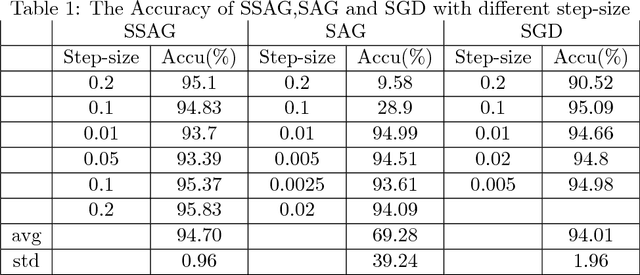
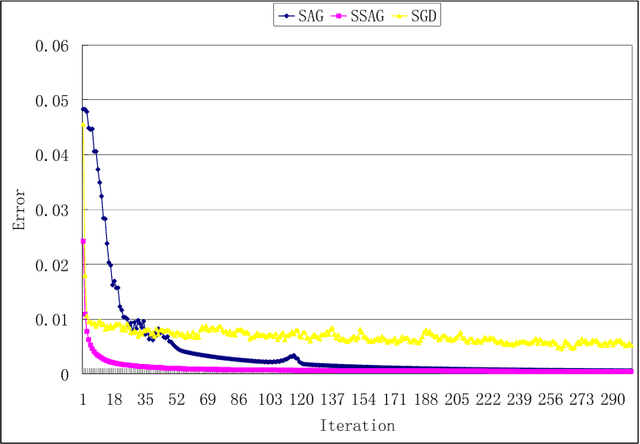
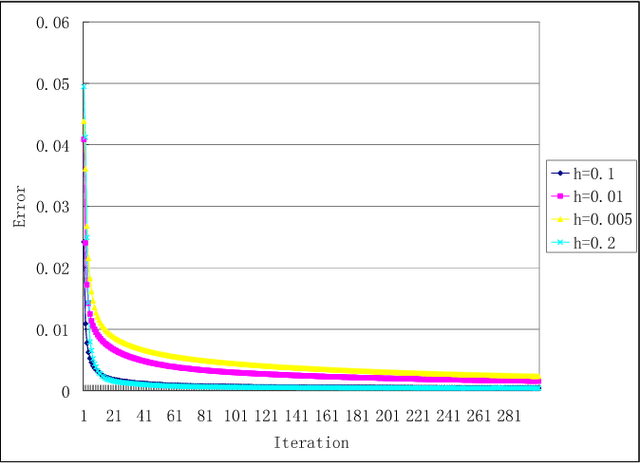
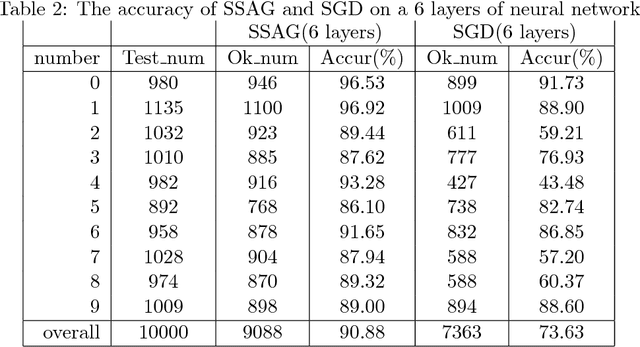
SGD (Stochastic Gradient Descent) is a popular algorithm for large scale optimization problems due to its low iterative cost. However, SGD can not achieve linear convergence rate as FGD (Full Gradient Descent) because of the inherent gradient variance. To attack the problem, mini-batch SGD was proposed to get a trade-off in terms of convergence rate and iteration cost. In this paper, a general CVI (Convergence-Variance Inequality) equation is presented to state formally the interaction of convergence rate and gradient variance. Then a novel algorithm named SSAG (Stochastic Stratified Average Gradient) is introduced to reduce gradient variance based on two techniques, stratified sampling and averaging over iterations that is a key idea in SAG (Stochastic Average Gradient). Furthermore, SSAG can achieve linear convergence rate of $\mathcal {O}((1-\frac{\mu}{8CL})^k)$ at smaller storage and iterative costs, where $C\geq 2$ is the category number of training data. This convergence rate depends mainly on the variance between classes, but not on the variance within the classes. In the case of $C\ll N$ ($N$ is the training data size), SSAG's convergence rate is much better than SAG's convergence rate of $\mathcal {O}((1-\frac{\mu}{8NL})^k)$. Our experimental results show SSAG outperforms SAG and many other algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge