A novel sampler for Gauss-Hermite determinantal point processes with application to Monte Carlo integration
Paper and Code
Mar 30, 2022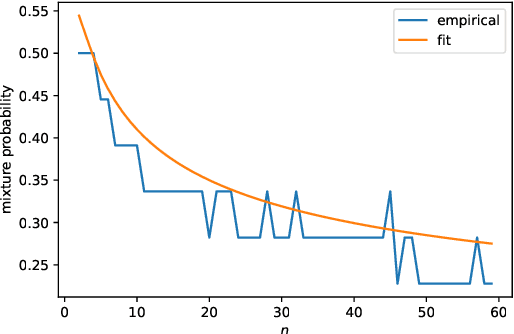
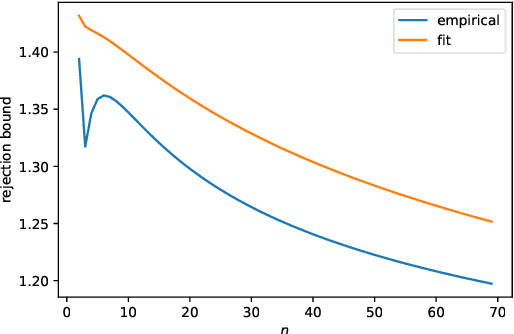
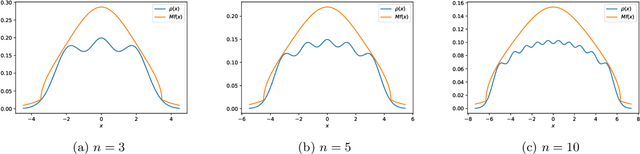
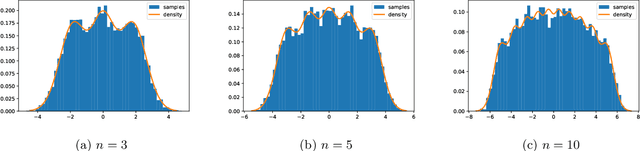
Determinantal points processes are a promising but relatively under-developed tool in machine learning and statistical modelling, being the canonical statistical example of distributions with repulsion. While their mathematical formulation is elegant and appealing, their practical use, such as simply sampling from them, is far from straightforward.Recent work has shown how a particular type of determinantal point process defined on the compact multidimensional space $[-1, 1]^d$ can be practically sampled and further shown how such samples can be used to improve Monte Carlo integration.This work extends those results to a new determinantal point process on $\mathbb{R}^d$ by constructing a novel sampling scheme. Samples from this new process are shown to be useful in Monte Carlo integration against Gaussian measure, which is particularly relevant in machine learning applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge