A Novel Higher-order Weisfeiler-Lehman Graph Convolution
Paper and Code
Jul 01, 2020
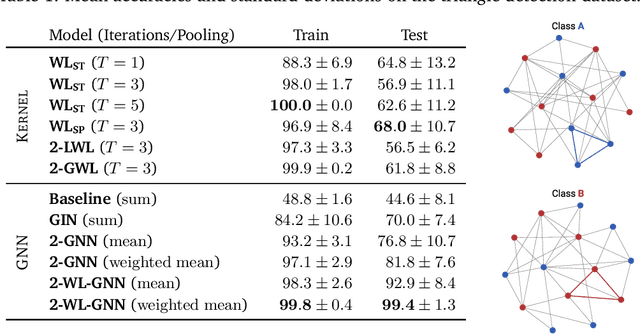

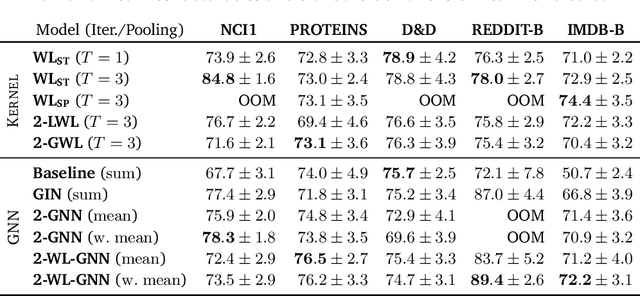
Current GNN architectures use a vertex neighborhood aggregation scheme, which limits their discriminative power to that of the 1-dimensional Weisfeiler-Lehman (WL) graph isomorphism test. Here, we propose a novel graph convolution operator that is based on the 2-dimensional WL test. We formally show that the resulting 2-WL-GNN architecture is more discriminative than existing GNN approaches. This theoretical result is complemented by experimental studies using synthetic and real data. On multiple common graph classification benchmarks, we demonstrate that the proposed model is competitive with state-of-the-art graph kernels and GNNs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge