A novel geometrically inspired polynomial kernel for robot inverse dynamics

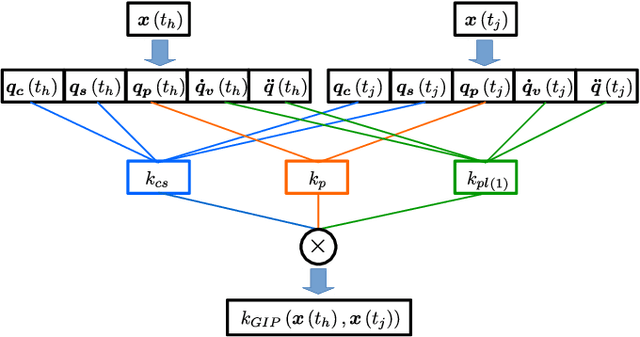
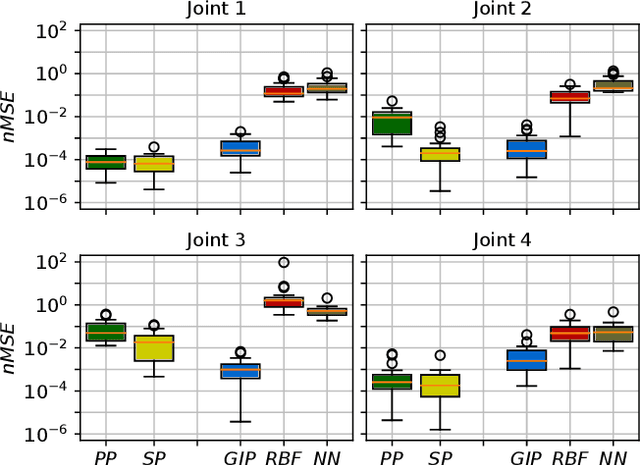
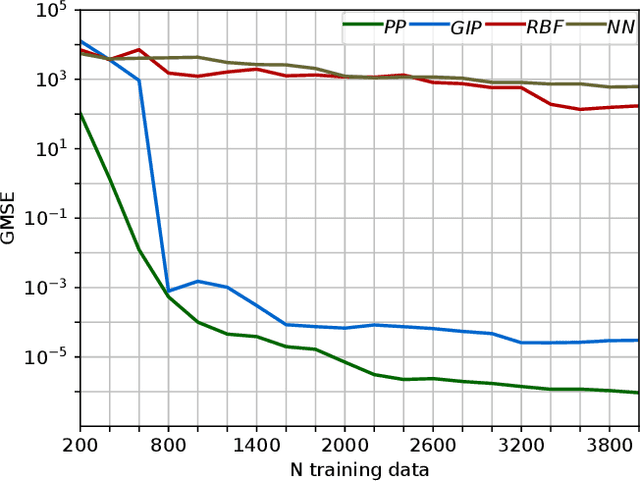
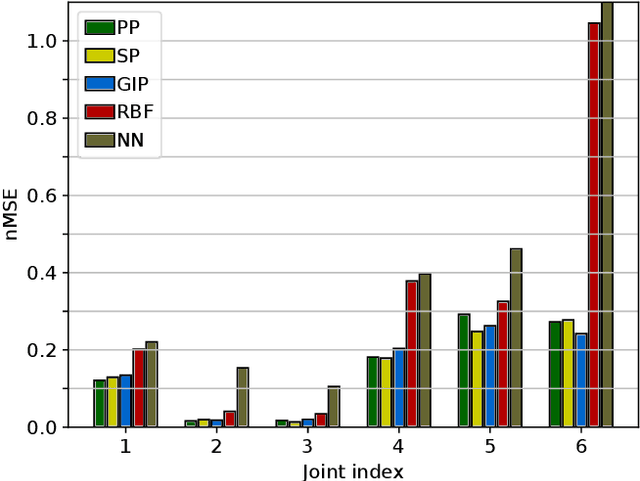
In this paper we introduce a novel data driven inverse dynamics estimator based on Gaussian Process Regression. Driven by the fact that the inverse dynamics can be described as a polynomial function on a suitable input space, we propose the use of a novel kernel, called Geometrically Inspired Polynomial Kernel (GIP). The resulting estimator behaves similarly to model based approaches as concerns data efficiency. Indeed, we proved that the GIP kernel defines a finite dimensional Reproducing Kernel Hilbert Space that contains the inverse dynamics function computed through the Rigid Body Dynamics. The proposed kernel is based on the recently introduced Multiplicative Polynomial Kernel, a redefinition of the classical polynomial kernel equipped with a set of parameters which allows for an higher regularization. We tested the proposed approach in a simulated environment, and also in real experiments with a UR10 robot. The obtained results confirm that, compared to other data driven estimators, the proposed approach is more data efficient and exhibits better generalization properties. Instead, with respect to model based estimators, our approach requires less prior information and is not affected by model bias.