A Normative Model of Classifier Fusion

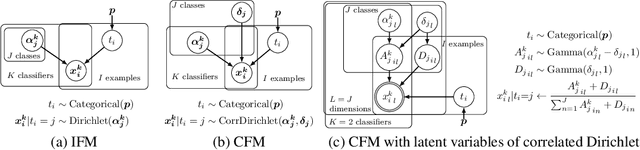
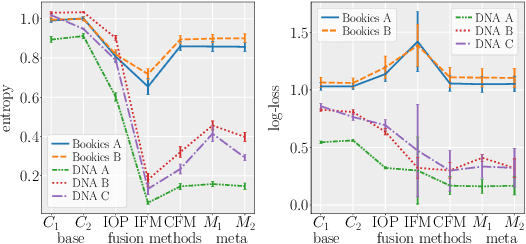
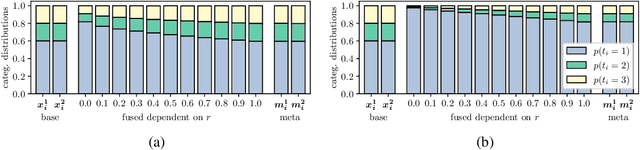
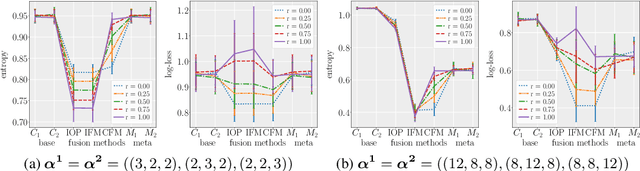
Combining the outputs of multiple classifiers or experts into a single probabilistic classification is a fundamental task in machine learning with broad applications from classifier fusion to expert opinion pooling. Here we present a hierarchical Bayesian model of probabilistic classifier fusion based on a new correlated Dirichlet distribution. This distribution explicitly models positive correlations between marginally Dirichlet-distributed random vectors thereby allowing normative modeling of correlations between base classifiers or experts. The proposed model naturally accommodates the classic Independent Opinion Pool and other independent fusion algorithms as special cases. It is evaluated by uncertainty reduction and correctness of fusion on synthetic and real-world data sets. We show that a change in performance of the fused classifier due to uncertainty reduction can be Bayes optimal even for highly correlated base classifiers.