A Nonparametric Approach to 3D Shape Analysis from Digital Camera Images - I. in Memory of W.P. Dayawansa

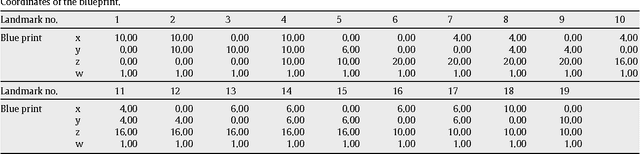
In this article, for the first time, one develops a nonparametric methodology for an analysis of shapes of configurations of landmarks on real 3D objects from regular camera photographs, thus making 3D shape analysis very accessible. A fundamental result in computer vision by Faugeras (1992), Hartley, Gupta and Chang (1992) is that generically, a finite 3D configuration of points can be retrieved up to a projective transformation, from corresponding configurations in a pair of camera images. Consequently, the projective shape of a 3D configuration can be retrieved from two of its planar views. Given the inherent registration errors, the 3D projective shape can be estimated from a sample of photos of the scene containing that configuration. Projective shapes are here regarded as points on projective shape manifolds. Using large sample and nonparametric bootstrap methodology for extrinsic means on manifolds, one gives confidence regions and tests for the mean projective shape of a 3D configuration from its 2D camera images.