A Nonlinear Constrained Optimization Framework for Comfortable and Customizable Motion Planning of Nonholonomic Mobile Robots - Part I
Paper and Code
May 22, 2013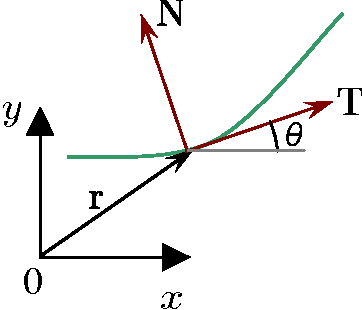
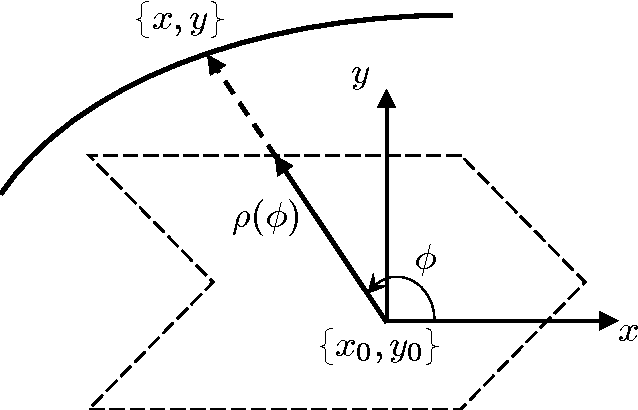
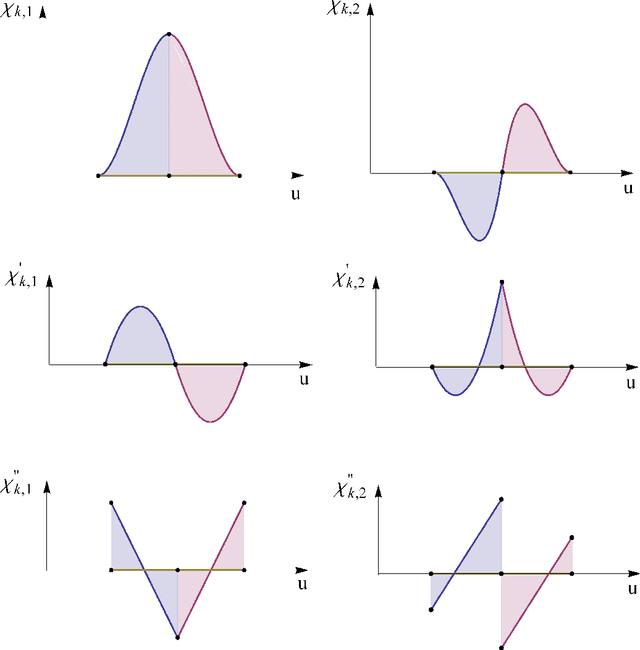
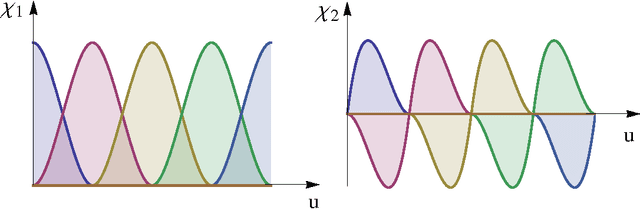
In this series of papers, we present a motion planning framework for planning comfortable and customizable motion of nonholonomic mobile robots such as intelligent wheelchairs and autonomous cars. In this first one we present the mathematical foundation of our framework. The motion of a mobile robot that transports a human should be comfortable and customizable. We identify several properties that a trajectory must have for comfort. We model motion discomfort as a weighted cost functional and define comfortable motion planning as a nonlinear constrained optimization problem of computing trajectories that minimize this discomfort given the appropriate boundary conditions and constraints. The optimization problem is infinite-dimensional and we discretize it using conforming finite elements. We also outline a method by which different users may customize the motion to achieve personal comfort. There exists significant past work in kinodynamic motion planning, to the best of our knowledge, our work is the first comprehensive formulation of kinodynamic motion planning for a nonholonomic mobile robot as a nonlinear optimization problem that includes all of the following - a careful analysis of boundary conditions, continuity requirements on trajectory, dynamic constraints, obstacle avoidance constraints, and a robust numerical implementation. In this paper, we present the mathematical foundation of the motion planning framework and formulate the full nonlinear constrained optimization problem. We describe, in brief, the discretization method using finite elements and the process of computing initial guesses for the optimization problem. Details of the above two are presented in Part II of the series.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge