A Nonlinear Constrained Optimization Framework for Comfortable and Customizable Motion Planning of Nonholonomic Mobile Robots - Part II
Paper and Code
May 22, 2013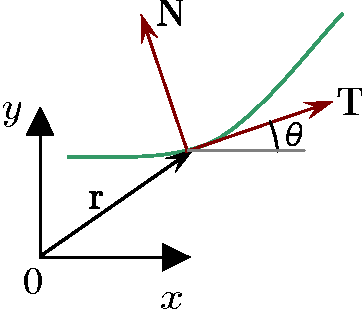
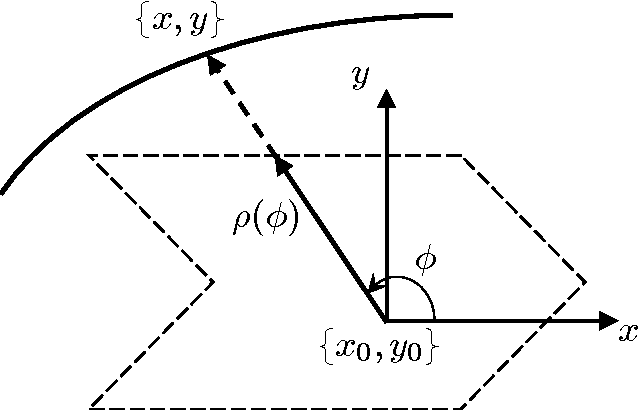
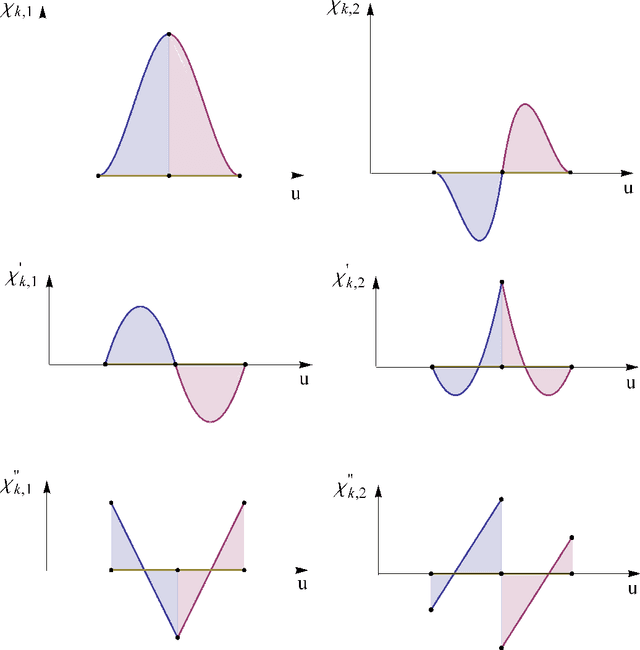
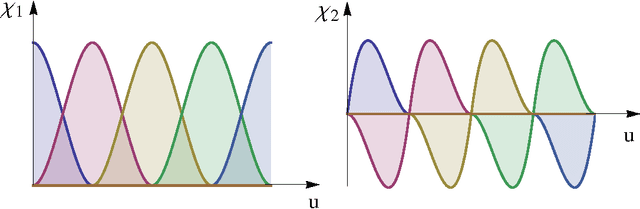
In this series of papers, we present a motion planning framework for planning comfortable and customizable motion of nonholonomic mobile robots such as intelligent wheelchairs and autonomous cars. In Part I, we presented the mathematical foundation of our framework, where we model motion discomfort as a weighted cost functional and define comfortable motion planning as a nonlinear constrained optimization problem of computing trajectories that minimize this discomfort given the appropriate boundary conditions and constraints. In this paper, we discretize the infinite-dimensional optimization problem using conforming finite elements. We describe shape functions to handle different kinds of boundary conditions and the choice of unknowns to obtain a sparse Hessian matrix. We also describe in detail how any trajectory computation problem can have infinitely many locally optimal solutions and our method of handling them. Additionally, since we have a nonlinear and constrained problem, computation of high quality initial guesses is crucial for efficient solution. We show how to compute them.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge