A New Characterization of Probabilities in Bayesian Networks
Paper and Code
Jul 11, 2012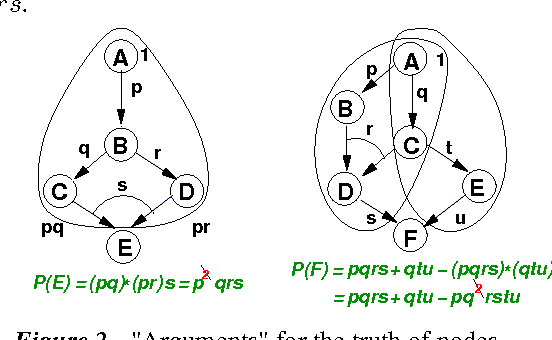
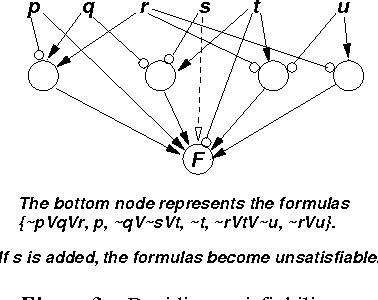
We characterize probabilities in Bayesian networks in terms of algebraic expressions called quasi-probabilities. These are arrived at by casting Bayesian networks as noisy AND-OR-NOT networks, and viewing the subnetworks that lead to a node as arguments for or against a node. Quasi-probabilities are in a sense the "natural" algebra of Bayesian networks: we can easily compute the marginal quasi-probability of any node recursively, in a compact form; and we can obtain the joint quasi-probability of any set of nodes by multiplying their marginals (using an idempotent product operator). Quasi-probabilities are easily manipulated to improve the efficiency of probabilistic inference. They also turn out to be representable as square-wave pulse trains, and joint and marginal distributions can be computed by multiplication and complementation of pulse trains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge