A New Approach to Time-Optimal Path Parameterization based on Reachability Analysis
Paper and Code
Nov 22, 2017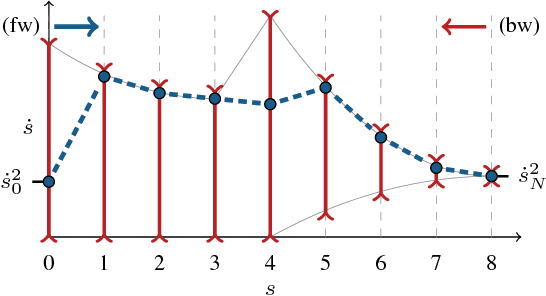
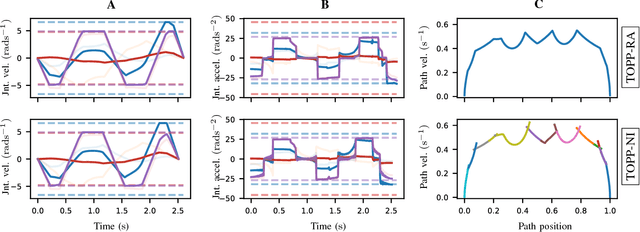
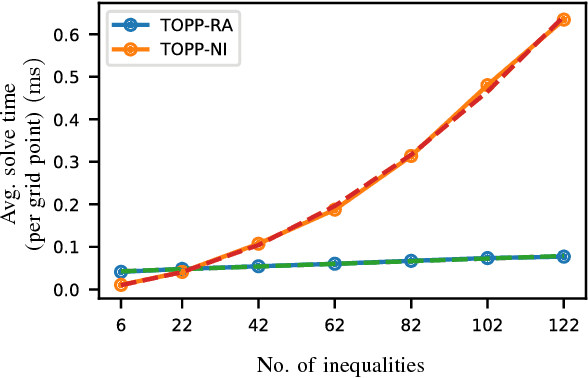
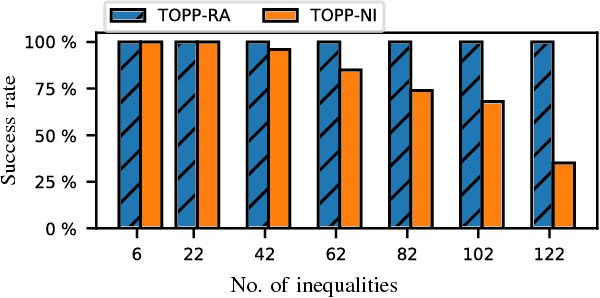
Time-Optimal Path Parameterization (TOPP) is a well-studied problem in robotics and has a wide range of applications. There are two main families of methods to address TOPP: Numerical Integration (NI) and Convex Optimization (CO). NI-based methods are fast but difficult to implement and suffer from robustness issues, while CO-based approaches are more robust but at the same time significantly slower. Here we propose a new approach to TOPP based on Reachability Analysis (RA). The key insight is to recursively compute reachable and controllable sets at discretized positions on the path by solving small Linear Programs (LPs). The resulting algorithm is faster than NI-based methods and as robust as CO-based ones (100% success rate), as confirmed by extensive numerical evaluations. Moreover, the proposed approach offers unique additional benefits: Admissible Velocity Propagation and robustness to parametric uncertainty can be derived from it in a simple and natural way.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge