A New Approach to 3D ICP Covariance Estimation for Mobile Robotics

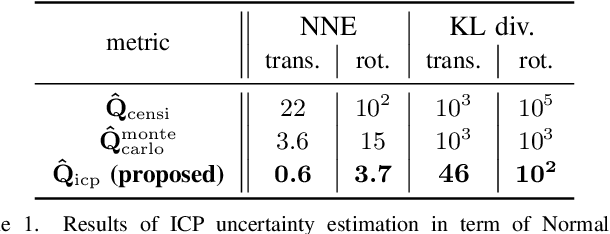
In mobile robotics, scan matching of point clouds using Iterative Closest Point (ICP) allows estimating sensor displacements. It may prove important to assess the associated uncertainty about the obtained rigid transformation, especially for sensor fusion purposes. In this paper we propose a novel approach to 3D ICP covariance computation that accounts for all the sources of errors as listed in Censi's pioneering work, namely wrong convergence, underconstrained situations, and sensor noise. Our approach builds on two facts. First, ICP is not a standard sensor: owing to wrong convergence the concept of ICP covariance per se is actually meaningless, as the dispersion in the ICP outputs may largely depend on the accuracy of the initialization, and is thus inherently related to the prior uncertainty on the displacement. We capture this using the unscented transform, which also reflects correlations between initial and final uncertainties. Then, assuming white sensor noise leads to overoptimism: ICP is biased, owing to e.g. calibration biases, which we account for. Our solution is tested on publicly available real data ranging from structured to unstructured environments, where our algorithm predicts consistent results with actual uncertainty, and compares very favorably to previous methods. We finally demonstrate the benefits of our method for pose-graph localization, where our approach improves accuracy and robustness of the estimates.