A Neural Network Approach for Online Nonlinear Neyman-Pearson Classification

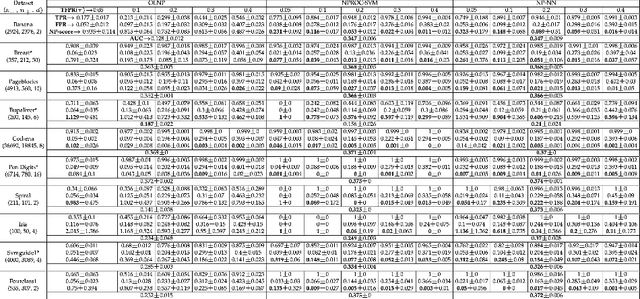
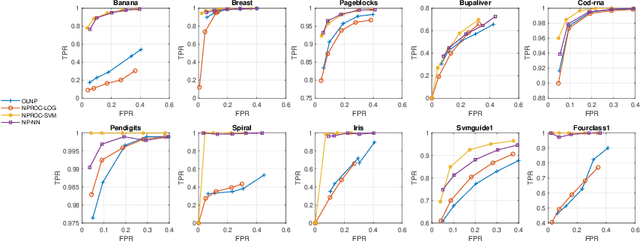
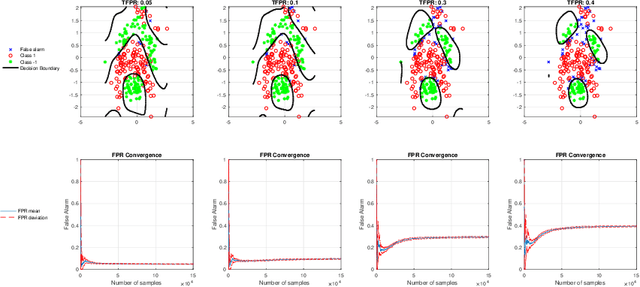
We propose a novel Neyman-Pearson (NP) classifier that is both online and nonlinear as the first time in the literature. The proposed classifier operates on a binary labeled data stream in an online manner, and maximizes the detection power about a user-specified and controllable false positive rate. Our NP classifier is a single hidden layer feedforward neural network (SLFN), which is initialized with random Fourier features (RFFs) to construct the kernel space of the radial basis function at its hidden layer with sinusoidal activation. Not only does this use of RFFs provide an excellent initialization with great nonlinear modeling capability, but it also exponentially reduces the parameter complexity and compactifies the network to mitigate overfitting while improving the processing efficiency substantially. We sequentially learn the SLFN with stochastic gradient descent updates based on a Lagrangian NP objective. As a result, we obtain an expedited online adaptation and powerful nonlinear Neyman-Pearson modeling. Our algorithm is appropriate for large scale data applications and provides a decent false positive rate controllability with real time processing since it only has O(N) computational and O(1) space complexity (N: number of data instances). In our extensive set of experiments on several real datasets, our algorithm is highly superior over the competing state-of-the-art techniques, either by outperforming in terms of the NP classification objective with a comparable computational as well as space complexity or by achieving a comparable performance with significantly lower complexity.