A Multi-view Dimensionality Reduction Algorithm Based on Smooth Representation Model
Paper and Code
Oct 12, 2019
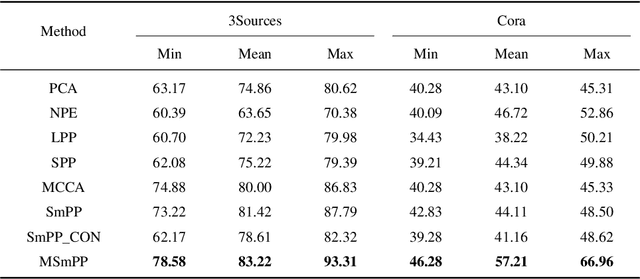


Over the past few decades, we have witnessed a large family of algorithms that have been designed to provide different solutions to the problem of dimensionality reduction (DR). The DR is an essential tool to excavate the important information from the high-dimensional data by mapping the data to a low-dimensional subspace. Furthermore, for the diversity of varied high-dimensional data, the multi-view features can be utilized for improving the learning performance. However, many DR methods fail to integrating multiple views. Although the features from different views are extracted by different manners, they are utilized to describe the same sample, which implies that they are highly related. Therefore, how to learn the subspace for high-dimensional features by utilizing the consistency and complementary properties of multi-view features is important in the present. In this paper, we propose an effective multi-view dimensionality reduction algorithm named Multi-view Smooth Preserve Projection. Firstly, we construct a single view DR method named Smooth Preserve Projection based on the Smooth Representation model. The proposed method aims to find a subspace for the high-dimensional data, in which the smooth reconstructive weights are preserved as much as possible. Then, we extend it to a multi-view version in which we exploits Hilbert-Schmidt Independence Criterion to jointly learn one common subspace for all views. A plenty of experiments on multi-view datasets show the excellent performance of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge