A hybrid neural-network and finite-difference method for solving Poisson equation with jump discontinuities on interfaces

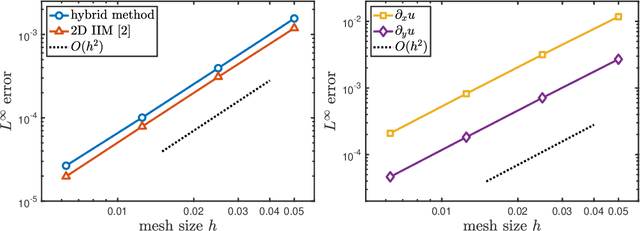
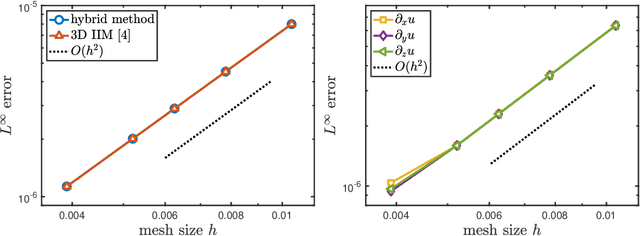
In this work, a new hybrid neural-network and finite-difference method is developed for solving Poisson equation in a regular domain with jump discontinuities on an embedded irregular interface. Since the solution has low regularity across the interface, when applying finite difference discretization to this problem, an additional treatment accounting for the jump discontinuities must be employed at grid points near the interface. Here, we aim to elevate such an extra effort to ease our implementation. The key idea is to decompose the solution into two parts: singular (non-smooth) and regular (smooth) parts. The neural network learning machinery incorporating given jump conditions finds the singular solution, while the standard finite difference method is used to obtain the regular solution with associated boundary conditions. Regardless of the interface geometry, these two tasks only require a supervised learning task of function approximation and a fast direct solver of the Poisson equation, making the hybrid method easy to implement and efficient. The two- and three-dimensional numerical results show that the present hybrid method preserves second-order accuracy for the solution and its derivatives, and it is comparable with the traditional immersed interface method in the literature.