A Functional-Space Mean-Field Theory of Partially-Trained Three-Layer Neural Networks
Paper and Code
Oct 28, 2022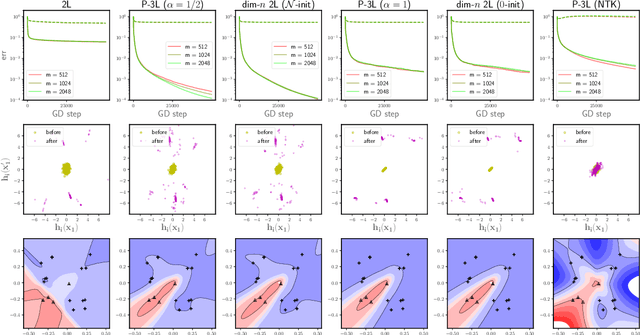
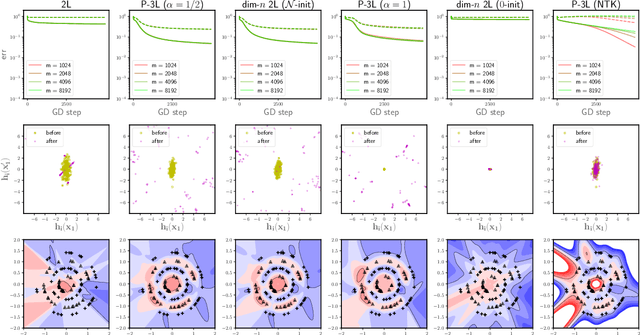
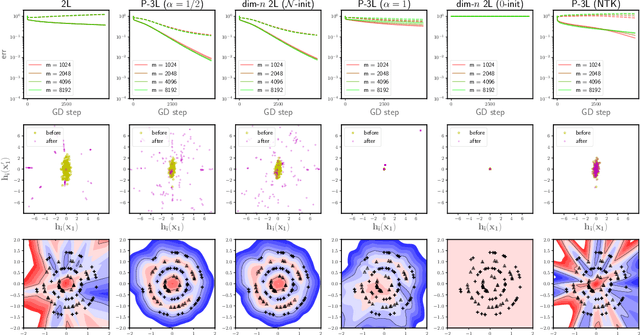
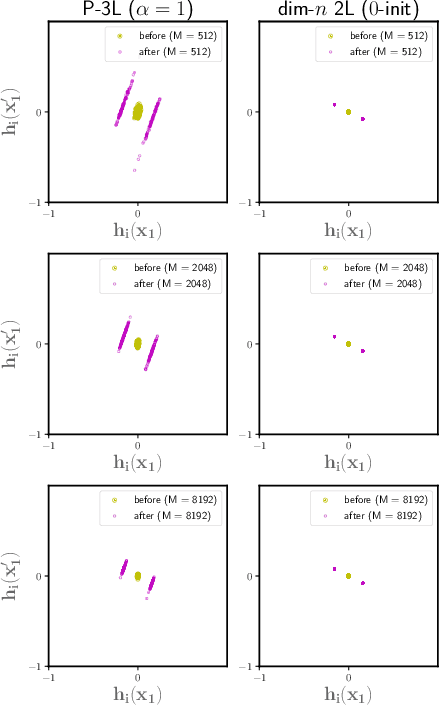
To understand the training dynamics of neural networks (NNs), prior studies have considered the infinite-width mean-field (MF) limit of two-layer NN, establishing theoretical guarantees of its convergence under gradient flow training as well as its approximation and generalization capabilities. In this work, we study the infinite-width limit of a type of three-layer NN model whose first layer is random and fixed. To define the limiting model rigorously, we generalize the MF theory of two-layer NNs by treating the neurons as belonging to functional spaces. Then, by writing the MF training dynamics as a kernel gradient flow with a time-varying kernel that remains positive-definite, we prove that its training loss in $L_2$ regression decays to zero at a linear rate. Furthermore, we define function spaces that include the solutions obtainable through the MF training dynamics and prove Rademacher complexity bounds for these spaces. Our theory accommodates different scaling choices of the model, resulting in two regimes of the MF limit that demonstrate distinctive behaviors while both exhibiting feature learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge