A Fully Polynomial Time Approximation Scheme for Fixed-Horizon Constrained Stochastic Shortest Path Problem under Local Transitions

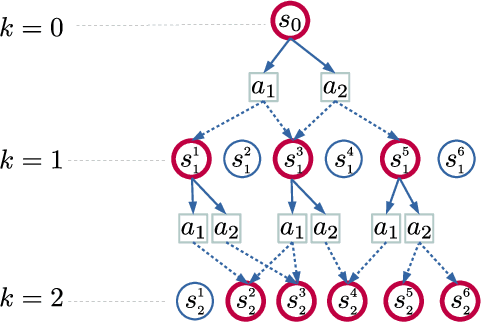
The fixed-horizon constrained stochastic shortest path problem (C-SSP) is a formalism for planning in stochastic environments under certain operating constraints. Chance-Constrained SSP (CC-SSP) is a variant that allows bounding the probability of constraint violation, which is desired in many safety-critical applications. This work considers an important variant of (C)C-SSP under local transition, capturing a broad class of SSP problems where state reachability exhibit a certain locality. Only a constant number of states can share some subsequent states. (C)C-SSP under local transition is NP-Hard even for a planning horizon of two. In this work, we propose a fully polynomial-time approximation scheme for (C)C-SSP that computes (near) optimal deterministic policies. Such an algorithm is the best approximation algorithm attainable in theory