A Fully Online Approach for Covariance Matrices Estimation of Stochastic Gradient Descent Solutions

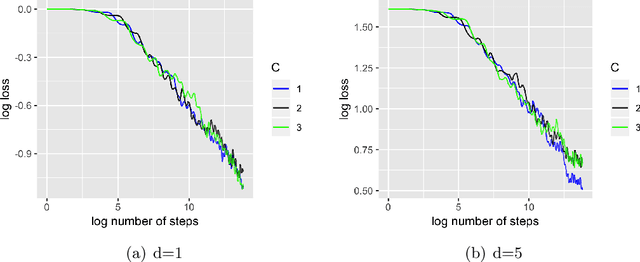
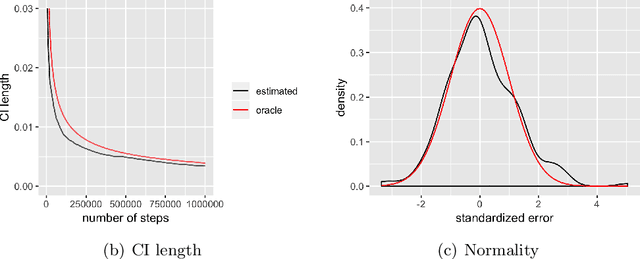
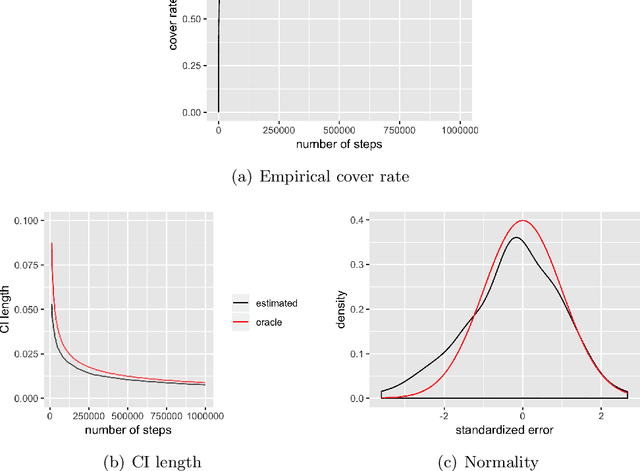
Stochastic gradient descent (SGD) algorithm is widely used for parameter estimation especially in online setting. While this recursive algorithm is popular for computation and memory efficiency, the problem of quantifying variability and randomness of the solutions has been rarely studied. This paper aims at conducting statistical inference of SGD-based estimates in online setting. In particular, we propose a fully online estimator for the covariance matrix of averaged SGD iterates (ASGD). Based on the classic asymptotic normality results of ASGD, we construct asymptotically valid confidence intervals for model parameters. Upon receiving new observations, we can quickly update the covariance estimator and confidence intervals. This approach fits in online setting even if the total number of data is unknown and takes the full advantage of SGD: efficiency in both computation and memory.