A forward differential deep learning-based algorithm for solving high-dimensional nonlinear backward stochastic differential equations
Paper and Code
Aug 10, 2024
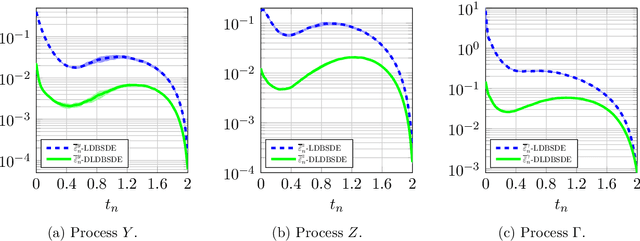


In this work, we present a novel forward differential deep learning-based algorithm for solving high-dimensional nonlinear backward stochastic differential equations (BSDEs). Motivated by the fact that differential deep learning can efficiently approximate the labels and their derivatives with respect to inputs, we transform the BSDE problem into a differential deep learning problem. This is done by leveraging Malliavin calculus, resulting in a system of BSDEs. The unknown solution of the BSDE system is a triple of processes $(Y, Z, \Gamma)$, representing the solution, its gradient, and the Hessian matrix. The main idea of our algorithm is to discretize the integrals using the Euler-Maruyama method and approximate the unknown discrete solution triple using three deep neural networks. The parameters of these networks are then optimized by globally minimizing a differential learning loss function, which is novelty defined as a weighted sum of the dynamics of the discretized system of BSDEs. Through various high-dimensional examples, we demonstrate that our proposed scheme is more efficient in terms of accuracy and computation time compared to other contemporary forward deep learning-based methodologies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge