A Flexible Framework for Multi-Objective Bayesian Optimization using Random Scalarizations

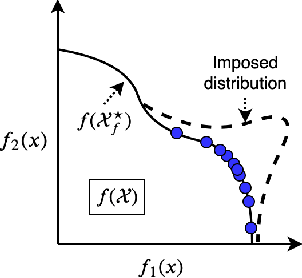
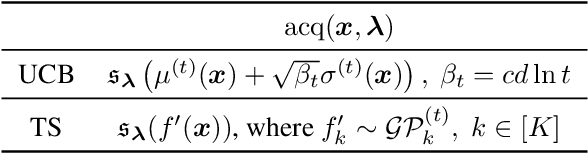
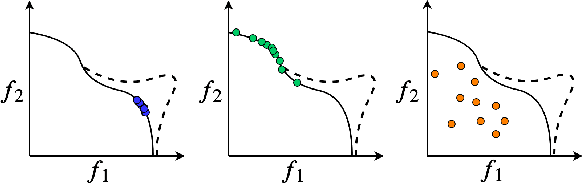
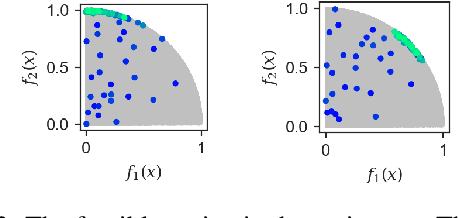
Many real world applications can be framed as multi-objective optimization problems, where we wish to simultaneously optimize for multiple criteria. Bayesian optimization techniques for the multi-objective setting are pertinent when the evaluation of the functions in question are expensive. Traditional methods for multi-objective optimization, both Bayesian and otherwise, are aimed at recovering the Pareto front of these objectives. However, in certain cases a practitioner might desire to identify Pareto optimal points only in a particular region of the Pareto front due to external considerations. In this work, we propose a strategy based on random scalarizations of the objectives that addresses this problem. While being computationally similar or cheaper than other approaches, our approach is flexible enough to sample from specified subsets of the Pareto front or the whole of it. We also introduce a novel notion of regret in the multi-objective setting and show that our strategy achieves sublinear regret. We experiment with both synthetic and real-life problems, and demonstrate superior performance of our proposed algorithm in terms of flexibility, scalability and regret.