A feature construction framework based on outlier detection and discriminative pattern mining
Paper and Code
Jul 17, 2014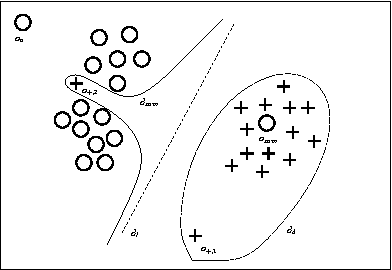
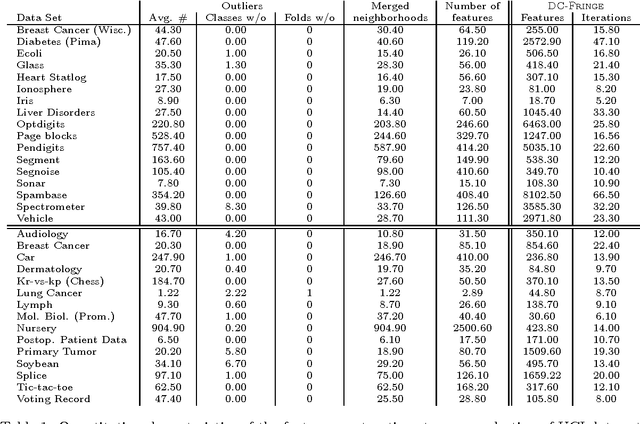
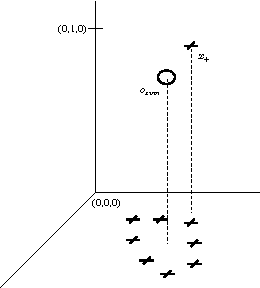
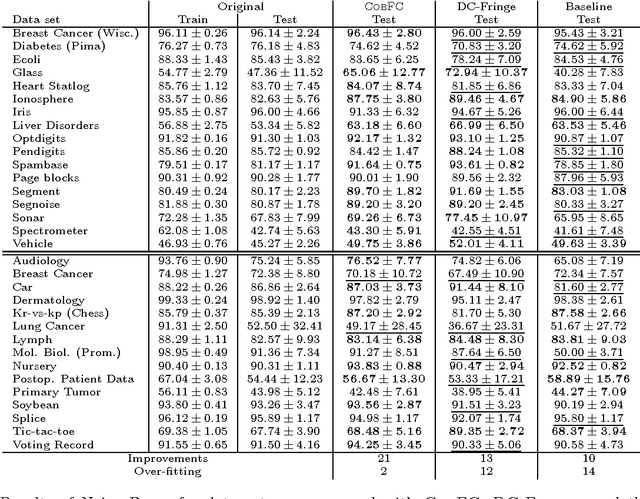
No matter the expressive power and sophistication of supervised learning algorithms, their effectiveness is restricted by the features describing the data. This is not a new insight in ML and many methods for feature selection, transformation, and construction have been developed. But while this is on-going for general techniques for feature selection and transformation, i.e. dimensionality reduction, work on feature construction, i.e. enriching the data, is by now mainly the domain of image, particularly character, recognition, and NLP. In this work, we propose a new general framework for feature construction. The need for feature construction in a data set is indicated by class outliers and discriminative pattern mining used to derive features on their k-neighborhoods. We instantiate the framework with LOF and C4.5-Rules, and evaluate the usefulness of the derived features on a diverse collection of UCI data sets. The derived features are more often useful than ones derived by DC-Fringe, and our approach is much less likely to overfit. But while a weak learner, Naive Bayes, benefits strongly from the feature construction, the effect is less pronounced for C4.5, and almost vanishes for an SVM leaner. Keywords: feature construction, classification, outlier detection
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge