A fast Multiplicative Updates algorithm for Non-negative Matrix Factorization
Paper and Code
Mar 31, 2023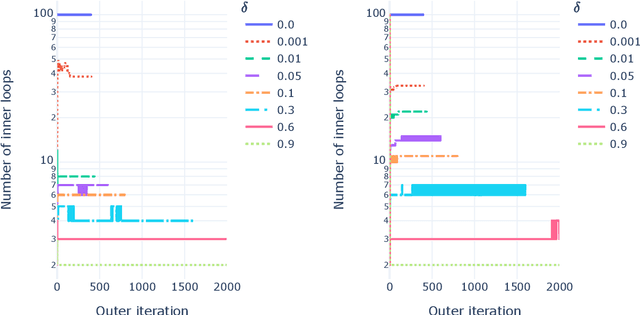



Nonnegative Matrix Factorization is an important tool in unsupervised machine learning to decompose a data matrix into a product of parts that are often interpretable. Many algorithms have been proposed during the last three decades. A well-known method is the Multiplicative Updates algorithm proposed by Lee and Seung in 2002. Multiplicative updates have many interesting features: they are simple to implement and can be adapted to popular variants such as sparse Nonnegative Matrix Factorization, and, according to recent benchmarks, is state-of-the-art for many problems where the loss function is not the Frobenius norm. In this manuscript, we propose to improve the Multiplicative Updates algorithm seen as an alternating majorization minimization algorithm by crafting a tighter upper bound of the Hessian matrix for each alternate subproblem. Convergence is still ensured and we observe in practice on both synthetic and real world dataset that the proposed fastMU algorithm is often several orders of magnitude faster than the regular Multiplicative Updates algorithm, and can even be competitive with state-of-the-art methods for the Frobenius loss.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge