A Dual-Dimer Method for Training Physics-Constrained Neural Networks with Minimax Architecture

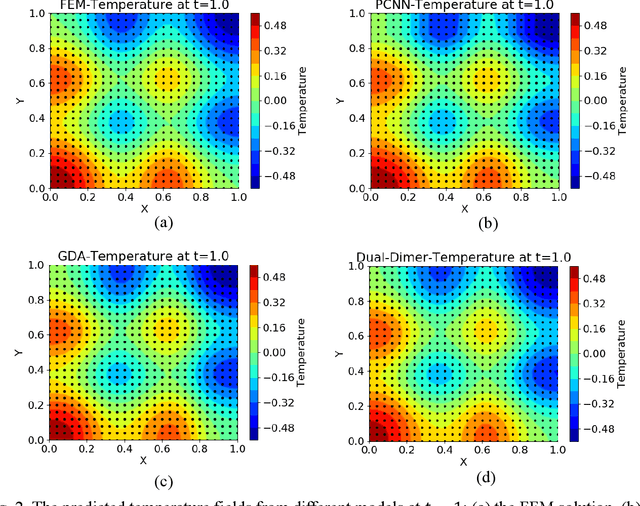
Data sparsity is a common issue to train machine learning tools such as neural networks for engineering and scientific applications, where experiments and simulations are expensive. Recently physics-constrained neural networks (PCNNs) were developed to reduce the required amount of training data. However, the weights of different losses from data and physical constraints are adjusted empirically in PCNNs. In this paper, a new physics-constrained neural network with the minimax architecture (PCNNMM) is proposed so that the weights of different losses can be adjusted systematically. The training of the PCNN-MM is searching the high-order saddle points of the objective function. A novel saddle point search algorithm called Dual-Dimer method is developed. It is demonstrated that the Dual-Dimer method is computationally more efficient than the gradient descent ascent method for nonconvex-nonconcave functions and provides additional eigenvalue information to verify search results. A heat transfer example also shows that the convergence of PCNN-MMs is faster than that of traditional PCNNs.