A distribution-free mixed-integer optimization approach to hierarchical modelling of clustered and longitudinal data
Paper and Code
Feb 06, 2023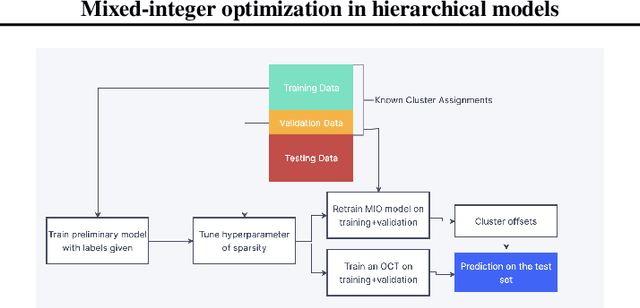



We create a mixed-integer optimization (MIO) approach for doing cluster-aware regression, i.e. linear regression that takes into account the inherent clustered structure of the data. We compare to the linear mixed effects regression (LMEM) which is the most used current method, and design simulation experiments to show superior performance to LMEM in terms of both predictive and inferential metrics in silico. Furthermore, we show how our method is formulated in a very interpretable way; LMEM cannot generalize and make cluster-informed predictions when the cluster of new data points is unknown, but we solve this problem by training an interpretable classification tree that can help decide cluster effects for new data points, and demonstrate the power of this generalizability on a real protein expression dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge