A Discrete Empirical Interpolation Method for Interpretable Immersion and Embedding of Nonlinear Manifolds
Paper and Code
May 21, 2019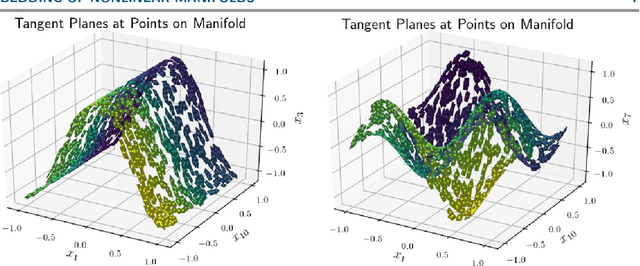
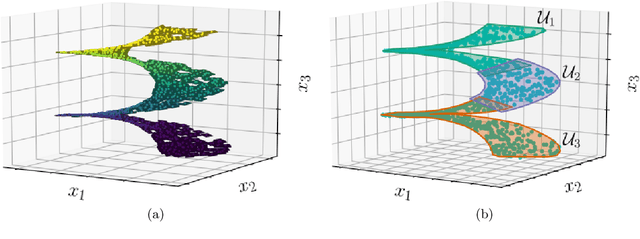
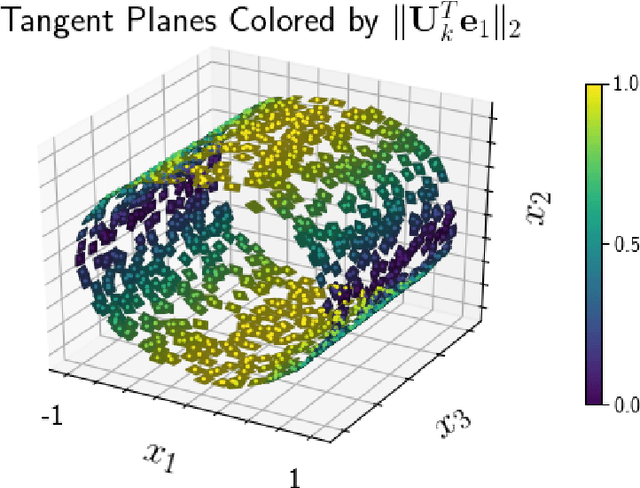
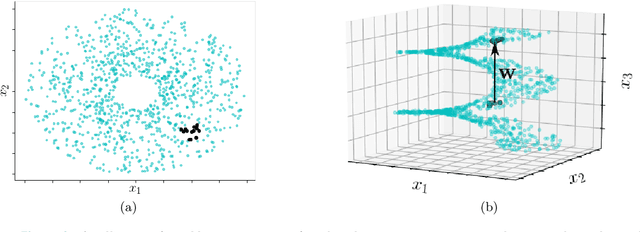
Manifold learning techniques seek to discover structure-preserving mappings of high-dimensional data into low-dimensional spaces. While the new sets of coordinates specified by these mappings can closely parameterize the data, they are generally complicated nonlinear functions of the original variables. This makes them difficult to interpret physically. Furthermore, in data-driven model reduction applications the governing equations may have structure that is destroyed by nonlinear mapping into coordinates on an inertial manifold, creating a computational bottleneck for simulations. Instead, we propose to identify a small collection of the original variables which are capable of uniquely determining all others either locally via immersion or globally via embedding of the underlying manifold. When the data lies on a low-dimensional subspace the existing discrete empirical interpolation method (DEIM) accomplishes this with recent variants employing greedy algorithms based on pivoted QR (PQR) factorizations. However, low-dimensional manifolds coming from a variety of applications, particularly from advection-dominated PDEs, do not lie in or near any low-dimensional subspace. Our proposed approach extends DEIM to data lying near nonlinear manifolds by applying a similar pivoted QR procedure simultaneously on collections of patches making up locally linear approximations of the manifold, resulting in a novel simultaneously pivoted QR (SimPQR) algorithm. The immersion provided by SimPQR can be extended to an embedding by applying SimPQR a second time to a modified collection of vectors. The SimPQR method for computing these `nonlinear DEIM' (NLDEIM) coordinates is successfully applied to real-world data lying near an inertial manifold in a cylinder wake flow as well as data coming from a viscous Burgers equation with different initial conditions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge